Espace préhilbertien - Définition

Introduction

En mathématiques, un espace préhilbertien est défini comme un espace vectoriel réel ou complexe muni d'un produit scalaire. Cette notion généralise celles d'espace euclidien ou hermitien, en omettant l'hypothèse de la dimension finie.

Motivations

Le cas général d'un espace préhilbertien en dimension infinie diffère à bien des égards de la dimension finie. L'espace dual n'est plus nécessairement isomorphe à l'espace, l'orthogonal d'un sous-espace vectoriel n'est plus nécessairement un supplémentaire de ce sous-espace, l'orthogonal de l'orthogonal d'un sous-espace ne redonne pas nécessairement ce sous-espace. Par ailleurs, les applications linéaires ne sont plus nécessairement continues. Les techniques d'analyse de l'espace sont en conséquence un peu différentes. Les cas de dimension finie sont traités dans les articles Espace euclidien et Espace hermitien. Le cas général est l'objet essentiel de cet article.

Une application importante est l'étude des espaces de fonctions à l'aide des outils de l'algèbre linéaire et bilinéaire. Le produit scalaire est donné par l'intégrale du produit de deux fonctions, ou plus précisément d'une fonction et du conjugué de l'autre pour conserver le caractère sesquilinéaire. A la différence du cas de la dimension finie, le produit scalaire n'est plus toujours défini, au sens où l'image du couple (x,x) peut être nulle même si x est un vecteur non nul. Une intégrale ne dépend en effet pas des valeurs de la fonction sur un ensemble de mesure nulle. Le terme utilisé est semi-produit scalaire. Une précision est généralement donnée : l'espace est séparable, c'est-à-dire qu'il existe une famille de vecteurs dénombrable et dense dans l'espace. Cette configuration correspond à nombre d'espaces fonctionnels.

Un outil permet de pallier la difficulté induite par la dimension infinie, la topologie. Le produit scalaire définit une norme, par voie de conséquence une distance et une topologie. Si le caractère spécifique que confère le produit scalaire à l'espace métrique permet la démonstration de nombreux résultats, une propriété fait néanmoins défaut. Le préfixe "pré-" apparaissant dans le mot préhilbertien fait référence à l'absence d'une hypothèse particulière : la complétude, qui se révèle indispensable pour de nombreux résultats. Lorsque cette hypothèse est vérifiée, l'espace porte le nom d'espace hilbertien ou Hilbert.

De nombreux espaces fonctionnels naturels ne sont pas complets, par exemple l'espace des fonctions continues à support compact. Il existe une manière simple de compléter un préhilbertien, à l'aide de son dual. Une démarche fréquente consiste à enrichir l'espace préhilbertien pour disposer de résultats puissants.

Propriétés

Topologie

Comme pour l'étude des différents espaces fonctionnels, l'absence d'hypothèse sur la dimension impose l'utilisation de nouveaux outils. L'essentiel des techniques de la dimension finie s'avère en effet inopérant. La topologie induite par le produit scalaire est suffisamment spécifique pour établir d'importants résultats. L'analyse de cette topologie dans le cadre général des espaces vectoriel normés montre qu'elle est compatible avec les lois de composition de l'espace vectoriel. Pour être précis, l'addition, la multiplication externe et la norme sont continues pour cette topologie. Les boules ouvertes de centre un point x de l'espace forment une base de voisinages, elles sont convexes.

Elles possèdent une propriété supplémentaire. Les boules sont bien arrondies : les segments suffisamment longs inclus dans une boule ont leur milieu relativement loin du bord. Cette propriété s'exprime de la manière suivante :

Ici, B(1,0) désigne la boule de rayon un et de centre le vecteur nul. Cette propriété ne confère pas au préhilbertien le statut d'espace uniformément convexe car il n'est pas nécessairement complet.

C'est une conséquence de l'identité du parallélogramme. Il suffit de remarquer que :

 

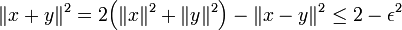
Sous-espace et espace produit

Tout sous-espace vectoriel d'un préhilbertien est un préhilbertien pour la restriction du produit scalaire.

Soit E et F deux préhilbertiens, alors le produit scalaire <.,.>_ExF défini par l'égalité suivante, confère au produit ExF le statut d'espace préhilbertien :

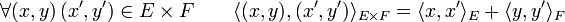
Espace quotient

Soit F un sous-espace fermé de E, l'analyse générale des espaces vectoriels normés montre que E/F est un espace vectoriel normé pour la norme suivante :

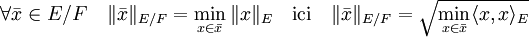
Dans le cas d'un préhilbertien, cette norme dispose d'une propriété forte :

• La norme issue du quotient de E est associée à un produit scalaire. Il est donné par la formule suivante :

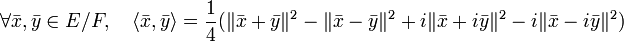
Ainsi, le quotient est aussi un espace préhilbertien.

Cette configuration est analogue dans le cas d'un semi-produit scalaire. L'analyse d'une semi-norme montre que l'ensemble des vecteurs de semi-norme nulle est un sous-espace vectoriel fermé. Cette propriété amène à la définition suivante :

• Le noyau d'un semi-produit scalaire est l'ensemble des vecteurs orthogonaux à l'espace entier.

Encore une fois, la configuration analysée pour les semi-normes est compatible avec celles des préhilbertiens non séparés.

• Le noyau d'un semi-produit scalaire est le noyau de la semi-norme associé.

Ainsi, un vecteur est de semi-norme nulle si et seulement s'il est orthogonal avec tous les vecteurs de l'espace. Comme pour le cas des semi-normes, il devient possible de quotienter un préhilbertien non séparé par le noyau du semi-produit scalaire :

• Le quotient d'un préhilbertien non séparé par le noyau du semi-produit scalaire est un préhilbertien séparé.

Comme dans le cas des espaces vectoriels munis d'une semi-norme, cette technique est utilisée en analyse fonctionnelle pour disposer d'un espace séparé. Un exemple est donné par les fonctions F nulles en dehors de Ω et intégrables (au sens de Riemann, c'est bien suffisant). Pour éviter les difficultés liées aux intégrales impropres, on peut supposer de plus que Ω est bornée. Le semi-produit scalaire naturel est le suivant :

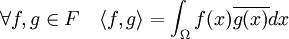
Le noyau F₀ du semi-produit scalaire est composé des fonctions de F nulles partout sauf peut-être sur un ensemble négligeable de Ω. Cet ensemble est l'orthogonal de F. Le quotient de F par F₀ désigne l'ensemble de classes de fonctions intégrables et nulles en dehors de Ω et qui ne diffèrent que sur un ensemble de mesure nulle.

• La norme issue du quotient de E est associée à un produit scalaire. Il est donné par la formule suivante :

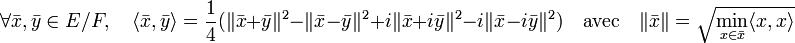
• Le noyau du semi-produit scalaire est le noyau E₀ de la semi-norme associée :

Soit x₀ un élément de E₀, y un élément de E et t un réel. La semi-norme de x₀ + t.y est toujours positive, donc :

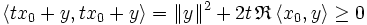
Le fait que l'égalité précédente soit positive pour toute valeur de t montre que la partie réelle du semi-produit scalaire de x₀ et y est nulle. Le même calcul appliqué à i.y, si i désigne l'imaginaire pure montre que la partie imaginaire du semi-produit scalaire est aussi nulle. Réciproquement, tout élément du noyau du semi-produit scalaire est orthogonal à l'ensemble entier dont à lui-même et fait donc partie du noyau de la semi-norme, ce qui termine la démonstration.

• Le quotient d'un préhilbertien son séparé par le noyau du semi-produit scalaire est un préhilbertien séparé.

Cette propriété est générale à toute semi-norme, (cf. l'article semi-norme).

 

Base

L'un des attraits d'un préhilbertien réside dans le fait que, sous des hypothèses très générales, il existe une base de Hilbert ayant des propriétés proches de celle d'une base au sens algébrique du terme.

A la différence de la dimension finie, il n'est plus possible d'exprimer un vecteur comme une somme ne comportant qu'un nombre fini de termes non nuls. Le vecteur apparaît comme la limite d'une série dont l'ensemble des termes non nuls est dénombrable. En revanche la convergence étant absolue, l'ordre de la série n'a guère d'importance.

L'existence n'est pas toujours garantie. En revanche, elle est assurée à l'aide du lemme de Zorn si l'espace est complet. Et, à l'image de tous les espaces vectoriels normés, il est relativement simple de compléter un préhilbertien.

Cette existence assurée par la complétude n'est pas totalement satisfaisante. L'utilisation de l'axiome du choix dans le lemme de Zorn rend la méthode inutilisable pour une construction effective d'une telle base. En revanche le théorème de Stone-Weierstrass montre que de nombreux espaces fonctionnels sont séparables. Cette hypothèse supplémentaire est suffisante pour garantir l'existence d'une base de Hilbert sans l'utilisation de l'axiome du choix. Le Procédé de Gram-Schmidt permet de construire effectivement une telle base. Les polynômes trigonométriques ou ceux de Legendre sont des exemples pour l'espace des fonctions sur un segment des nombres réels, de carrés intégrable au sens de Lebesgue.

Complétude

Il est possible de compléter un espace vectoriel normé. Pour être précis, il existe un K espace vectoriel normé H et J une isométrie linéaire injective de E dans H tel que l'image de E par J soit dense dans H. Si M est un réel strictement positif, produit scalaire est une application uniformément continue du produit cartésien de la boule de rayon M avec elle même dans K. Comme K est un espace complet, car les réels et les complexes le sont, il se prolonge par continuité sur cette boule. Comme il n'existe qu'un unique prolongement par continuité (cf. l'article Continuité uniforme), pour deux vecteurs, ce prolongement ne dépend pas de la boule les contenant tous deux. Enfin, comme tout couple de vecteurs est inclus dans une boule, il est possible de prolonger le produit scalaire sur H.

La racine carrée du prolongement du produit scalaire appliquée sur deux fois le même vecteur est un prolongement par continuité de la norme. L'unicité de ce prolongement montre que J est une isométrie d'espace préhilbertien.

Opérateur borné

Les opérateurs bornés sont ceux par lesquels l'image de la boule unité est bornée. Ce sont les opérateurs continus. Sur un préhilbertien complexe on a la propriété suivante :

• Soient a un opérateur sur un préhilbertien complexe E, et b la borne supérieure de la fonction de la boule unité dans R₊ qui à x associe |<a(x), x>|. Alors la majoration suivante est vérifiée :

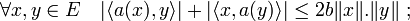
• en particulier
  • si b est fini alors a est borné ;
  • si, pour tout x élément de E, a(x) est orthogonal à x, alors a est nul.

Sur un préhilbertien réel, ce résultat n'est pas vrai. (Un contre-exemple est fourni, dans le plan, par une rotation d'un quart de tour.)

Il est utilisé par exemple pour l'étude des opérateurs compacts autoadjoints.

Supposons que x et y sont de norme 1 et démontrons que

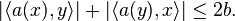
On calcule d'abord (en développant le membre de gauche) :

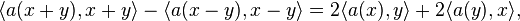
d'où (en utilisant l'identité du parallélogramme et l'hypothèse sur x et y) :

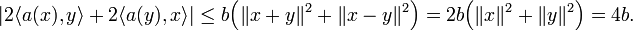
Soient θ₁, θ₂ des arguments respectifs des complexes <a(x),y> et <a(y),x>. Pour tout angle μ, les arguments correspondants de <a(x), exp(iμ)y> et de <a(exp(iμ)y),x> sont respectivement θ₁-μ et θ₂+μ, donc sont égaux si l'on choisit μ=(θ₁ - θ₂)/2. En remplaçant y par exp(iμ)y dans la majoration précédente, on obtient alors l'inégalité recherchée :

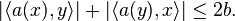
Structure du dual

Le dual possède des propriétés essentielles, à l'origine de la spécificité de la norme euclidienne (issue du produit scalaire) par rapport à une norme quelconque. Les conséquences sont aussi multiples que profondes. Ici, le terme "dual" est à prendre au sens topologique, c'est-à-dire que ne sont étudiées que les formes linéaires continues. Le dual est ainsi un espace vectoriel normé par la norme d'opérateur.

Tout d'abord, il possède la propriété, a priori manquante à E et pourtant si nécessaire :

• L'espace dual est complet.

Ensuite, le dual contient l'espace E et E est dense dans son dual. Il possède ainsi un rôle analogue aux nombres réels vis à vis des rationnels :

• L'application canonique φ de E dans son dual est une injection, son image est dense.

De plus, sa norme naturelle est le prolongement par continuité de celle de E. La norme en tant qu'opérateur de tout élément de E, identifié à une forme linéaire, correspond à la racine de la forme quadratique du produit scalaire de l'élément en tant que membre de E.

• L'application canonique φ de E dans son dual est une isométrie (si l'ensemble d'arrivé considéré est l'image φ) de E muni de la norme du produit scalaire vers son dual muni de la norme d'opérateur.

• Le produit scalaire de E se prolonge sur son dual par continuité. Ce prolongement est un produit scalaire tel que la norme associée confère un statut d'espace de Hilbert au dual.

Il existe ainsi une autre manière de compléter E, il suffit de l'identifier à une partie de son dual. Le dual est alors le complété. Comme il n'existe qu'une complétion à un isomorphisme isométrique près, cette méthode donne un résultat équivalent à la méthode générique de complétion d'un espace vectoriel normé. Le dual est complet et uniformément convexe, le théorème de Milman–Pettis montre qu'il est alors réflexif. Il possède néanmoins des propriétés plus fortes, développées dans l'article Espace de Hilbert.

• L'espace dual est complet.

Un élément du dual est une application linéaire continue dans un espace euclidien (de dimension un ou deux), or l'ensemble des applications linéaires continues d'un espace vectoriel normé dans un espace euclidien est complet. (la démonstration est donnée dans l'article Espace euclidien.)

• L'application canonique φ de E dans son dual est une injection, son image est dense.

Rappelons la définition de φ. A tout élément x de E, elle associe la forme linéaire qui à y associe <x, y>. L'image est clairement une forme linéaire. L'inégalité de Cauchy-Schwarz garantie sa continuité, sa norme est inférieure ou égale à celle de x. Un élément du noyau est orthogonal à E, or E est séparé, si l'image de x est nulle, sa norme est aussi nulle et x est donc nul ,ce qui montre que φ est injectif.

Le caractère dense de l'image provient d'un raisonnement analogue à celui démontrant le théorème de meilleure approximation. Soit δ une forme linéaire continue non nulle (si elle est nulle elle est alors dans l'image de φ car φ(0) = δ). L'objectif est de trouver un vecteur y tel que la distance entre δ et φ(y) soit inférieure à un ε donnée.

Il existe un vecteur v de E tel que δ(v) est égal à un. Soit H le noyau de φ, c'est un hyperplan, il est fermé car δ est continu. Soit λ la distance entre v et H, elle n'est pas nulle car sinon il existerait une suite d'éléments du noyau convergeant vers v, l'image de la suite par φ serait nulle et par continuité celle de v, ce qui n'est pas le cas. Soit ε un réel strictement positif et h un élément de H tel que le carré de la distance entre v et h soit inférieure à λ²(1 + ε²/2) et soit u et y les vecteur définis par :

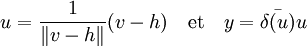
Il ne reste plus qu'à montrer que y et le vecteur recherché. Pour cela, il suffit de montrer que la valeur absolue de la différence des images d'un vecteur x de la sphère unité par δ et φ(y) est inférieure à ε.

On remarque que la droite engendrée par u et l'hyperplan H sont supplémentaires car H est un hyperplan et u n'est pas contenu dans H, donc il existe un réel α et un vecteur k de H tel que x = αu + k. Calculons le produit scalaire de y et de x :

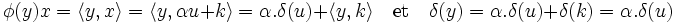
On en déduit que :

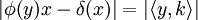
Le carré de la distance entre v et h - t.k est supérieure au carré de la distance entre v et H donc , si R désigne la partie réelle d'un nombre imaginaire :

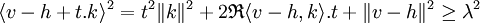
Or le carré de la distance entre v et h est majorée par λ² + ε²/2, donc :

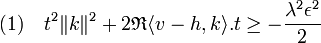
L'expression précédente est celle d'un polynôme de degré deux dont le monôme dominant est positif. Il atteint son minimum au point de dérivée nulle, pour la valeur de t₀ définie par :

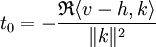
Pour cette valeur de t₀, la majoration (1) devient :

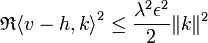
La norme de k est inférieure à celle de x, qui est égale à un donc :

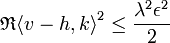
Le même calcul en remplaçant t par i.t, où i désigne l'imaginaire pur montre une égalité de même nature, on en déduit :

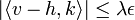
En remarquant que λ est plus grand que la norme de v - h, on obtient :

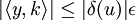
Ce qui montre la proximité de δ et φ(y) et permet de conclure.

• L'application canonique φ de E dans son dual est une isométrie (si l'ensemble d'arrivé considéré est l'image φ) de E muni de la norme du produit scalaire vers son dual :

Cette proposition revient à dire que les deux normes d'un vecteur x de E, donnée par le produit scalaire et par la norme d'opérateur sur φ(x) sont les mêmes. L'inégalité de Cauchy-Schwarz montre que la norme de x en temps qu'opérateur est inférieur ou égale à celle de x par le produit scalaire. L'égalité s'obtient en appliquant à φ(x) au vecteur x.

• Le produit scalaire de E se prolonge sur son dual par continuité :

Il est en effet possible de transporter le produit scalaire sur l'image de E par l'application φ. Sur l'image de E, les deux normes : celle des opérateurs et celle du produit scalaire sont confondue. Soit M un réel strictement positif. Sur la boule de centre le vecteur nul et de rayon M, le produit scalaire est une application uniformément continue. Elle possède donc un unique prolongement car l'ensemble d'arrivé est complet. Comme toute paire de vecteur est incluse dans une boule de centre le vecteur nul, il est possible de prolonger par continuité le produit scalaire sur E entier. L'unicité du prolongement assure que le choix de la boule n'influe pas sur le résultat.

• Ce prolongement est un produit scalaire tel que la norme associée confère un statut d'espace complet au dual :

Les normes associées au produit scalaire et à celle des opérateurs sont confondues sur un espace dense. Ces deux applications sont continues et donc confondues sur tout le dual. La norme des opérateurs confère au dual une structure d'espace complet, il en est de même pour celle du produit scalaire.