Faisceau gaussien - Définition
La liste des auteurs de cet article est disponible ici.
Propagation des faisceaux gaussiens
Le champ électrique complexe d'un faisceau gaussien mesuré (en volts par mètre) à

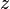
Et la distribution de l'intensité moyenne temporelle (ou radiance), mesurée en watts par mètre carré est:
Où:
-
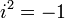
-
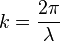
-
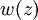
- E0 et I0 sont respectivement l'amplitude et l'intensité du champ électrique au centre du faisceau à l'origine. C'est-à-dire
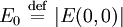
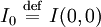
-
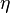
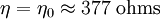
Puissance et intensité
Puissance par une ouverture
La puissance P (en watts) passant par un trou de rayon r dans un plan transverse à la propagation et à une distance z est:
-
![P(r,z) = P_0 \left[ 1 - e^{-2r^2 / w^2(z)} \right]\qquad \begin{cases} \end{cases}](https://static.techno-science.net/illustration/Definitions/autres/2/2865664a4a5d912292431d6799e66b2b_ef81deda21a8e8eccda5e02300149bb9.png)
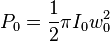
On trouve que:
- Pour un trou de rayon
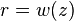
- Environ 95% de la puissance du faisceau passera par un trou ayant
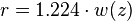
Intensité moyenne et maximale
L'intensité maximale sur l'axe du faisceau à
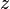

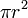
NOTA: La puissance maximale est donc le double de la puissance moyenne obtenue par la division de la puissance totale par w2(z).
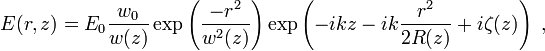
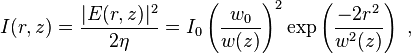
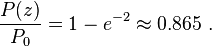
![I(0,z) =\lim_{r\to 0} \frac {P_0 \left[ 1 - e^{-2r^2 / w^2(z)} \right]} {\pi r^2} = \frac{P_0}{\pi} \lim_{r\to 0} \frac { \left[ -(-2)(2r) e^{-2r^2 / w^2(z)} \right]} {w^2(z)(2r)} = {2P_0 \over \pi w^2(z)}.](https://static.techno-science.net/illustration/Definitions/autres/b/b04fe4abc878b8ca997a6387281f9b8b_e6bd00560b90d4e5a5feab9ebac215c9.png)

















































