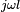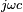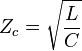Impédance caractéristique - Définition
L'impédance caractéristique d'une ligne de transmission idéale (c'est-à-dire sans perte) est définie par
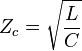
où L et C sont respectivement l'inductance et la capacité par unité de longueur de la ligne. Elle est indiquée dans les catalogues des constructeurs. Elle dépend :
- des dimensions des conducteurs, et de leur espacement ;
- de la constante diélectrique de l'isolant, dans la ligne coaxiale.
Valeurs typiques de l'impédance caractéristique :
- 50 ou 75 Ohms pour une ligne coaxiale ;
- 300 ohms pour une ligne bifilaire.
L'utilisation d'une ligne de transmission est principalement la transmission d'énergie électrique qui par une modulation appropriée supporte une information. La bonne transmission de cette information suppose le bon transfert de l'énergie ce qui suppose une bonne adaptation des impédances à l'entrée et la sortie du câble. Cette bonne adaptation se produit quand l'impédance des terminaisons est égale à l'impédance caractéristique du câble. Dans le cas contraire le transfert d'énergie n'est pas total et l'énergie non transférée fait demi tour ce qui présente des inconvénients par rapport au but recherché (à completer). Voir Adaptations d'impédances. C'est pour celà que quelques valeurs d'impédances caractéristiques ont été choisies pour faciliter le travail des concepteurs dans l'utilisation des câbles coaxiaux et de leur terminaison. (construction d'antennes, composants standards)
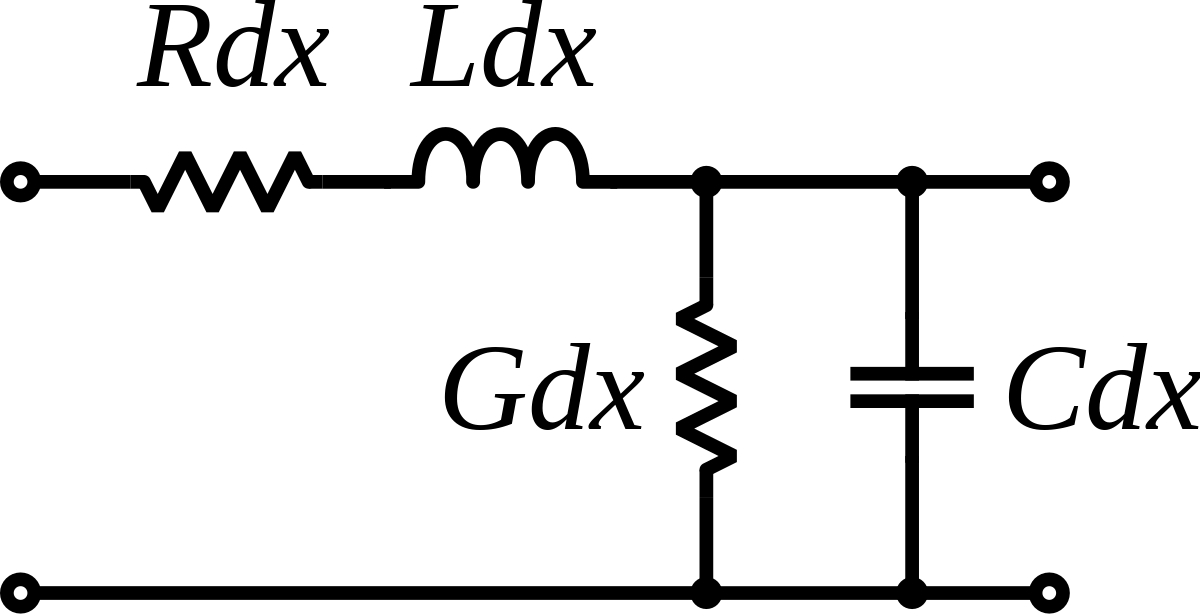
Pour une ligne de transmission réelle (avec pertes), l'impédance caractéristique est un nombre complexe :
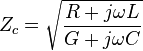
où R et G sont respectivement la résistance et la conductance de pertes par unité de longueur.
On remarque que à haute fréquence (