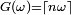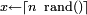Fonction de répartition - Définition
La liste des auteurs de cet article est disponible ici.
Conséquences du théorème de la réciproque
Simulation de variables aléatoires réelles de loi arbitraire
- Si
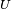
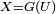
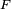
Ainsi dans tout langage de programmation possédant un générateur de nombres aléatoires, on peut simuler une suite de longueur arbitraire de v.a.r. indépendantes de même fonction de répartition
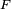
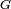
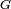
Exemples
| densité de probabilité | fonction de répartition | réciproque (généralisée) | code | |
|---|---|---|---|---|
| Loi de Cauchy |
|
|
|
|
| Loi exponentielle |
|
|
|
|
| Loi uniforme sur [a,b] |
|
|
|
|
| Loi de Bernoulli |
|
|
| |
| Loi uniforme sur
|
|
|
| |
| Loi normale, Loi binomiale | comme il n'y a pas de formule suffisamment explicite pour la fonction de répartition, et encore moins de formule explicite pour la réciproque de cette dernière, le théorème est alors inopérant. | |||
Autres conséquences du théorème de la réciproque
La réciproque généralisée de
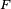
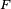
Théorème de la réciproque
Soit
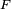
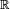
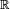
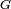
![\ \scriptstyle \omega \in]0,1[\](https://static.techno-science.net/illustration/Definitions/autres/4/4e14c719119402d051260b885dc74f70_bd8cd9dc869b561f12c49a67cdfff1c5.png)
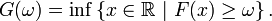
Alors
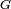
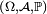
![\ \scriptstyle \left(\Omega,\mathcal{A}\right)=\left(]0,1[,\mathcal{B}(]0,1[)\right)\](https://static.techno-science.net/illustration/Definitions/autres/0/01ebc3908a0f4365553f75ec2ef257ec_4298454852665b809d7ef8dcb2593472.png)

![\ \scriptstyle \mathcal{B}(]0,1[)\](https://static.techno-science.net/illustration/Definitions/autres/0/0d41c4a896252b147406cbca239c0c4b_77a9035d84c1040c89edc790563cc6a6.png)
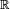
Théorème — Sur l'espace
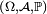
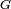
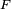
Ainsi toute fonction
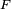
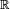
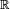
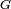
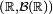
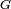
Démonstration
Pour
![\ \scriptstyle \omega \in \Omega=]0,1[\](https://static.techno-science.net/illustration/Definitions/autres/8/809bc065eb7f15f2d5eabdddb7f61c18_f8a0e48a85ae08269a14f1e0394a48d8.png)
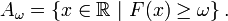
Donc
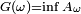
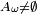
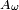
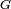
Commençons par un cas simple à titre d'entrainement:
F est continue strictement croissante
Si
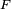
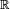
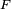
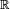
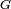
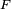
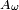
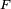
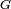
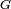
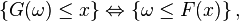
donc
![\begin{align} \left\{\omega\in\Omega\ |\ G(\omega)\le x\right\} &= \left\{\omega\in\Omega\ |\ \omega\le F(x)\right\} \\ &= ]0, F(x)]. \end{align}](https://static.techno-science.net/illustration/Definitions/autres/3/35865cf34891acce296bfba75db07b0a_ce46c9fba4a0604d6a52d3fded70d149.png)
Ainsi
![\mathbb{P}\left(G\le x\right) = \mathbb{P}(]0, F(x)]) =F(x).](https://static.techno-science.net/illustration/Definitions/autres/9/98fe2fd37fd2810bf1ff9d6a14f0c56f_fa6f5219bcc7acf9301cc16644d30730.png)
Cas général
Dans le cas général, on a également
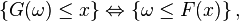
et on conclut donc exactement de la même manière que précédemment, mais la démonstration de l'équivalence ci-dessus est moins directe. Tout d'abord, pour
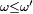
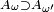
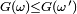
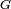
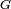
On a, par définition de
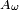
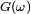
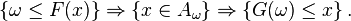
La réciproque vient de ce que
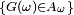
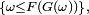
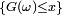
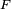
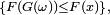
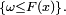
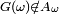
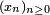
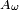
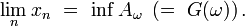
Par continuité à droite de
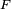
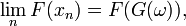
mais également, par définition de
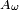
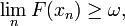
ce qui conduit à
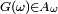
Remarques.
- Lorsque
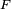

![\ \scriptstyle ]0,1[\](https://static.techno-science.net/illustration/Definitions/autres/0/0bb723693494c23859b5b32a93be9ee7_4615338a02e8da20206ec997d711a8c0.png)
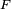
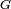
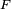
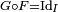
![\ \scriptstyle F\circ G=\text{Id}_{]0,1[}\](https://static.techno-science.net/illustration/Definitions/autres/a/a96a69b025c97cfff1156bca6707afba_c4a620b7fbf0437156c796db16a8ea78.png)
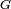
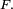
- L'intérêt pratique de ce Théorème est développé dans l'article Méthode de la transformée inverse, ainsi que dans la section suivante.
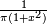
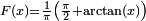
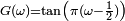
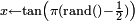
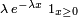
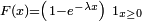
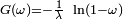
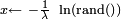
![\scriptstyle \frac{1}{b-a}\ 1_{[a,b]}(x)](https://static.techno-science.net/illustration/Definitions/autres/6/6f7f36df35625486b62d364b7ef0e3bd_5af6fe2a893c73289d0ac727f643c868.png)
![\scriptstyle F(x)=\frac{x-a}{b-a}\ 1_{[a,b]}(x)\ +\ 1_{]b,+\infty[}(x)](https://static.techno-science.net/illustration/Definitions/autres/1/1c678be4753c5a108f50b77bd6d99bf4_0ba53200db1c6b58748f75eb92271eec.png)
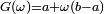
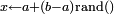
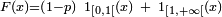
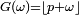
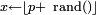
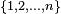
![\scriptstyle F(x)=\left\lfloor\frac{x}{n}\right\rfloor\ 1_{[0,1]}(x)\ +\ 1_{]1,+\infty[}(x)](https://static.techno-science.net/illustration/Definitions/autres/a/a4149ce6247bd14b4b417621e26c7bde_733dcb155a68aba237419d55394bb5d2.png)