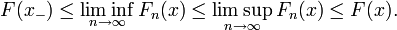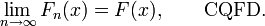Fonction de répartition - Définition
La liste des auteurs de cet article est disponible ici.
Convergence en loi et fonction de répartition
Considérons une suite de variables aléatoires
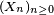

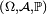
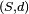
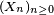

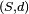
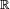
On a le théorème suivant :
Théorème — Dans le cas de variables aléatoires réelles (
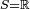
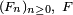
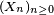
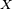
-
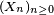
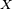
- pour tout réel

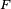
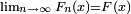
- il existe un espace probabilisé
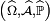
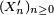
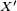
-
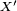
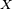
- pour chaque

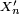
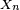
-
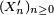
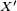
-
L'implication 1.
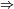
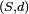
![\scriptstyle\ S=\mathcal{C}([0,1],\mathbb{R})\](https://static.techno-science.net/illustration/Definitions/autres/6/6bfa0c17e2d85d990761d80db4faf50e_4bc4a4cb8a250429cb11f468ca1437c2.png)
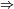
Une structure possible pour la démonstration est 3.
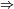
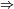
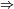
3. implique 1.
C'est le plus simple. Il faut démontrer que
ou bien, équivalemment,
Mais la continuité de
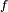
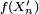
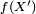
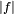
pour tout

1. implique 2.
On utilise la famille de fonctions continues bornées
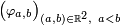
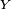
et en particulier
On remarque alors que, pour tout  ,
,
et
En faisant tendre

Ainsi, dès que

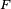
2. implique 3.
Notons
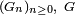
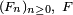
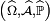
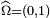
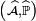
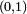
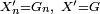
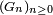
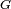
![\lim_{n\rightarrow\infty} \mathbb{E}\left[f(X_n)\right]=\mathbb{E}\left[f(X)\right],](https://static.techno-science.net/illustration/Definitions/autres/a/a9615e3f6607884ee583899e6b26d2d3_e1441d671648101fb12c7a1e8dcf189f.png)
![\lim_{n\rightarrow\infty} \mathbb{E}\left[f(X^{\prime}_n)\right]=\mathbb{E}\left[f(X^{\prime})\right].](https://static.techno-science.net/illustration/Definitions/autres/9/9520be37c6da8c06a3f309f6e4f5302d_7d84601abf2e0387a05fdf9a1b1ca379.png)
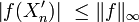
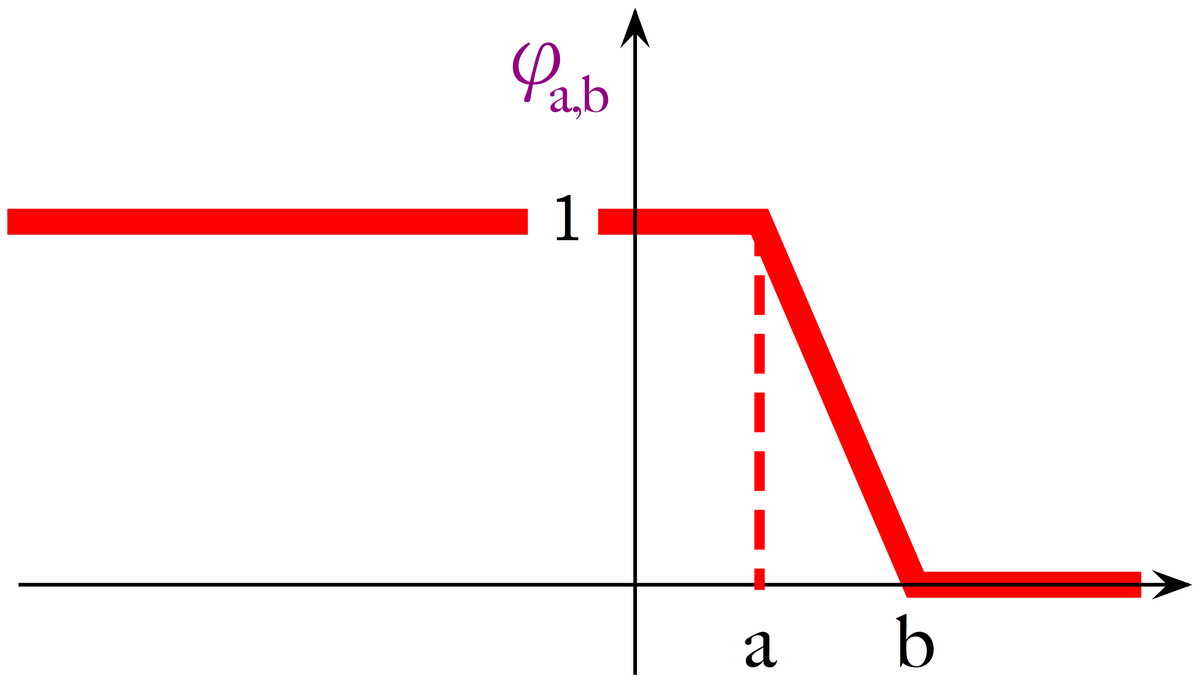
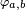
![\mathbb{P}\left(Y\le a\right) \le \mathbb{E}\left[\varphi_{a,b}(Y)\right] \le \mathbb{P}\left(Y\le b\right),](https://static.techno-science.net/illustration/Definitions/autres/3/38e77e6b67836cec541be22f6337ce93_f755bea554f28228109e2b5dc5391a7c.png)
![\mathbb{E}\left[\varphi_{x-\varepsilon,x}(X_n)\right] \le F_n(x) \le \mathbb{E}\left[\varphi_{x,x+\varepsilon}(X_n)\right].](https://static.techno-science.net/illustration/Definitions/autres/6/67b6e69b31d41500e1080c30af932a3b_1a39801c3bf08e423ea8fd4de38e0be2.png)
![\begin{align} \limsup_n F_n(x) &\le \lim_n\mathbb{E}\left[\varphi_{x,x+\varepsilon}(X_n)\right] \\ &= \mathbb{E}\left[\varphi_{x,x+\varepsilon}(X)\right] \le \mathbb{P}\left(X\le x+\varepsilon\right) = F(x+\varepsilon), \end{align}](https://static.techno-science.net/illustration/Definitions/autres/6/6f45eb7cb008df5a9d54391991bc0543_b7d83c586e00a12fc9dcd8f0e448a53c.png)
![\begin{align} \liminf_n F_n(x) &\ge \lim_n\mathbb{E}\left[\varphi_{x-\varepsilon,x}(X_n)\right] \\ &= \mathbb{E}\left[\varphi_{x-\varepsilon,x}(X)\right] \ge \mathbb{P}\left(X\le x-\varepsilon\right) = F(x-\varepsilon). \end{align}](https://static.techno-science.net/illustration/Definitions/autres/2/297e02e4d9179c2a7095d8b8f109a9da_e67809f333bf748a3015b62de185cc82.png)