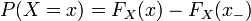Fonction de répartition - Définition
La liste des auteurs de cet article est disponible ici.
Caractérisation de la loi par la fonction de répartition
Théorème — La loi de probabilité d'une variable aléatoire réelle est caractérisée par sa fonction de répartition.
Ou bien encore : si deux variables aléatoires réelles ont même fonction de répartition, alors elles ont même loi (et réciproquement).
Sous l'hypothèse
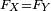
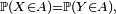
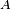
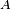
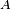
Il faut vérifier que
- la classe

- la tribu engendrée par

Le lemme d'unicité des probabilités permet alors de conclure.
Vérifions 1. Soit

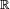


Vérifions 2. La tribu engendrée par

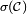
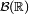
On a
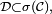
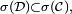

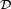
Comme
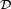
Mais il nous faut surtout démontrer l'inclusion en sens inverse, et, pour cela, démontrer que tout ouvert de
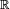
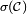
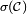
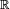
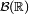
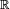
- tout ouvert de
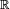
- les intervalles ouverts sont dans
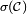
Le premier point résulte de ce que
- un ouvert
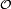
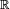
- les parties connexes de
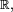
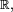
- comme
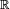
- dans chaque composante connexe
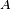
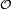
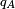
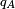
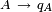
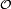
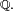
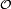
Le deuxième point tient à ce que
-
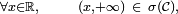
-
![\scriptstyle\forall y\in\mathbb{R},\qquad(-\infty,y)\ =\ \bigcup_{n\ge 1}\ \left(-\infty,y-\tfrac1n\right]\ \in\ \sigma (\mathcal{C})\](https://static.techno-science.net/illustration/Definitions/autres/3/32252fdd789e5127db4e92989c248077_9f6f273cf6113f5569bc9d189394e153.png)
-
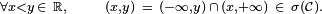
En d'autres termes, si deux variables aléatoires réelles,

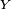
alors elles vérifient aussi que pour tout borélien
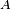
De plus, elles vérifient que pour toute fonction mesurable

dès que l'un des deux termes de l'égalite a un sens.
Propriétés de la fonction de répartition
Propriétés caractéristiques
Théorème — La fonction de répartition d'une variable aléatoire

-
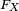
- Elle est partout continue à droite ;
-
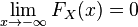
-
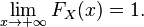
Le point 1 découle de la propriété de croissance des mesures de probabilité
![\{x\le y\}\Rightarrow\{]-\infty, x]\ \subset\ ]-\infty, y]\}\Rightarrow\{\mathbb{P}_{X}(]-\infty, x])\le\mathbb{P}_{X}(]-\infty, y])\}.](https://static.techno-science.net/illustration/Definitions/autres/b/b4c475303f5772c740862a3d88198d59_a20e769255f3afee69c43820385290d5.png)
Comme
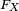
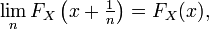
ou encore, équivalemment,
Mais les boréliens
![\scriptstyle \ \left]-\infty, x+\tfrac{1}{n}\right]\](https://static.techno-science.net/illustration/Definitions/autres/d/d160c4365d3625f7eebf900d2eb8101e_6331221f1cb1f813c7d9fb4657c43209.png)
![\bigcap_{n\ge 1}\left]-\infty, x+\tfrac1n\right]\ =\ \left]-\infty, x\right],](https://static.techno-science.net/illustration/Definitions/autres/f/ffad7c55f19bbad3e5270073a541c74e_9751647a346a6def5055139ee791cd28.png)
donc le point 2 est une conséquence des axiomes des probabilités. Comme
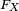
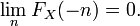
Ceci est encore une conséquence des axiomes des probabilités, puisque
![\bigcap_{n\ge 1}\left]-\infty, -n\right]\ =\ \emptyset.](https://static.techno-science.net/illustration/Definitions/autres/f/f9a54fdec983c67655f0bc598e48c6e3_b9a4ec399e38def122bb60a8c5540acd.png)
Le point 4 découle, de la même manière, de
![\bigcup_{n\ge 1}\left]-\infty, n\right]\ =\ \R.](https://static.techno-science.net/illustration/Definitions/autres/a/a6e48f3d1cc0a1b30c4dcdb4de99edc8_27cae99eabb0214d86df799880dd04fe.png)
Comme on l'a dit, les points 1 à 4 sont caractéristiques de la fonction de répartition d'une variable aléatoire réelle

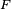

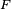
Autres propriétés
A cause des points 1, 3 et 4, FX est bornée, plus précisément
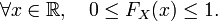
Comme toute fonction monotone bornée, FX admet en tout point x une limite à gauche FX (x— ) , limite à gauche égale ou non à FX (x) selon que FX est continue en x ou non.
La connaissance de la fonction de répartition permet de calculer la probabilité de tout intervalle
et
-
![\scriptstyle \ P(X \in ]- \infty;x])\,=\,P(X \le x)\,=\,F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/c/cbe11f392cb309a984784deebb39fced_2e90920feb91e9da2aa870f35780bf4e.png)
- on obtient
![\scriptstyle \ P(X \in ]x; + \infty[)\,=\,P(X >x)\,=\,1-F_X(x)\](https://upload.wikimedia.org/math/6/d/0/6d0e253476ff836e11594cbe61492d86.png) par passage au complémentaire,
par passage au complémentaire, - pour
![\scriptstyle \ P(X \in ]x;y])\,=\,P(x < X \le y)\,=\,F_X(y) - F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/9/94dd1431122d3a5c23bb2e895d78e0bf_1d8b48f655984b923a1af95e5706ed96.png)
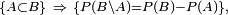
![\scriptstyle \ A=]- \infty;x]\](https://static.techno-science.net/illustration/Definitions/autres/8/81fba202958a5207fe1f320317bb9675_3de5f7b70024f9286f0418824b5219a4.png)
![\scriptstyle \ B=]- \infty;y],\](https://static.techno-science.net/illustration/Definitions/autres/1/1533dccb867647725c2a88b08f73716d_8064551c8e4e8489c0b8443f4133e114.png)
- La relation
![\scriptstyle \ P(X \in ]- \infty;x[)\,=\,P(X <x)\,=\,F_X(x_-),](https://static.techno-science.net/illustration/Definitions/autres/2/2afc20de164f23330b41035ff46c5c78_fead48cb9843a164a95bece146457fb1.png)
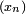
![\scriptstyle \ ]- \infty ; x[\](https://static.techno-science.net/illustration/Definitions/autres/f/f9e7fbc4f20f40047f968edc75a4c89c_21d347159a4db439684713d054141885.png)
![\scriptstyle \ ]- \infty ; x_{n}]](https://static.techno-science.net/illustration/Definitions/autres/3/3c90d17f4e0b367ec2375976360cb6fb_5a2aa46373d0e153ea0e48e252bf2d87.png)
![\scriptstyle \ ]- \infty ; x[\](https://static.techno-science.net/illustration/Definitions/autres/f/f9e7fbc4f20f40047f968edc75a4c89c_21d347159a4db439684713d054141885.png)
![\scriptstyle \ ]- \infty ; x_{n}]](https://static.techno-science.net/illustration/Definitions/autres/3/3c90d17f4e0b367ec2375976360cb6fb_5a2aa46373d0e153ea0e48e252bf2d87.png)
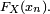
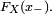
Les 5 dernières propriétés découlent de
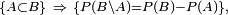
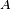
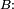
-
![\scriptstyle \ P(X \in ]x;y[ )\,=\,P(x < X < y)\,=\,F_X(y_-)-F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/0/00df5051e654ca256b129cbc6020a5e4_5c66571e6bc1b4d9fa2087d1c2cebba0.png)
![\scriptstyle \ A=]- \infty ; x],\quad \ B=]- \infty ; y[,\](https://static.techno-science.net/illustration/Definitions/autres/c/c7e00fbd07180c70bfb3efb66234f60f_22fdbf6a5263e5d33e36221746a9de6c.png)
-
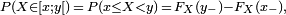
![\scriptstyle \ A=]- \infty ; x[,\quad \ B=]- \infty ; y[,\](https://static.techno-science.net/illustration/Definitions/autres/1/1f608e3c31907703f57bd3201caf4c45_a82da72b46fe04c5488b3fa6af399ebb.png)
-
![\scriptstyle \ P(X \in [x;y])\,=\,P(x \le X \le y)\,=\,F_X(y) - F_X(x_-),](https://static.techno-science.net/illustration/Definitions/autres/9/9f96d268f1bdd35241f9a205b3c129fd_c50bfea1f88d2aa8925a057acec4ffd3.png)
![\scriptstyle \ A=]- \infty ; x[,\quad \ B=]- \infty ; y],\](https://static.techno-science.net/illustration/Definitions/autres/b/b165412a7901ef8a22a3efbc2bde454d_bc3e85113a7ed9dad2c12b0efc60b9ac.png)
-
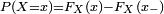
![\scriptstyle \ A=]- \infty ; x[,\quad \ B=]- \infty ; x].\](https://static.techno-science.net/illustration/Definitions/autres/8/8a27b572521996269d19951ed866bd3d_e56197b1c57e4b3c3fd75a6bb2d944cd.png)
On appelle atome de la variable aléatoire X tout réel a pour lequel ![\scriptstyle \ P[X=a]>0](https://upload.wikimedia.org/math/3/5/1/351883ce7e7ade6bdd61ed0ef8401650.png) . Ainsi, en vertu de la dernière propriété de la liste ci-dessus,
. Ainsi, en vertu de la dernière propriété de la liste ci-dessus,
Propriété — Les atomes de la variable aléatoire X sont exactement les points de discontinuité de la fonction de répartition.
La fonction de répartition d'une variable aléatoire X est donc continue si et seulement si X n'a aucun atome, i.e. si et seulement si
![\forall x\in\mathbb{R},\ P[X = x]=0.](https://static.techno-science.net/illustration/Definitions/autres/c/c10069f9caf35ebbdf66ee3a950c5986_ec7141f7b1faa368a2d4d47a8ebe2de0.png)
On dit alors que la loi de X est diffuse, ou bien sans atome, et, par extension, que la variable aléatoire X elle-même est diffuse ou sans atome. En particulier, les variables aléatoires réelles possédant une densité de probabilité sont diffuses. Il existe cependant des variables aléatoires diffuses mais ne possédant pas pour autant une densité de probabilité, c'est le cas, par exemple, de la variable aléatoire ayant pour fonction de répartition l'escalier de Cantor.
Notons que l'ensemble des points de discontinuité de FX est fini ou dénombrable, comme c'est le cas pour toute fonction monotone bornée :
Conséquence — L'ensemble S des atomes de la variable aléatoire X est fini ou dénombrable.
![\mathcal{C}=\left\{(-\infty,x]\ |\ x\in\mathbb{R}\right\}.](https://static.techno-science.net/illustration/Definitions/autres/8/824c50068bcfc140b8f1239e2035170c_a7c35e2ff961d3d05ac7240340ae5562.png)
![\bigcap_{x\in I}(-\infty,x]\,=\,(-\infty,y]\ \in\ \mathcal{C}.](https://static.techno-science.net/illustration/Definitions/autres/7/7952beeabcc2bdb7e4adec85b51dce25_98d010e971dd7449a09f552c10360cd7.png)
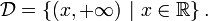
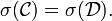
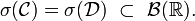
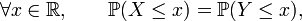
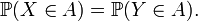
![\ \qquad \mathbb{E}[\varphi(X)]=\mathbb{E}[\varphi(Y)],](https://static.techno-science.net/illustration/Definitions/autres/4/4cf91938d6d9b4e99480c9c2a118f03f_cce8d4a733a9068fc96ce94d58b00e9a.png)
![P(X \in ]- \infty;x])\,=\,P(X \le x)\,=\,F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/9/964b972abf0511deccbfe1385e6808e2_047968b153ac6a07a12a736bb7f68a5c.png)
![P(X \in ]x; + \infty[)\,=\,P(X >x)\,=\,1-F_X(x),](https://upload.wikimedia.org/math/e/5/9/e59ebbcc8b457959cbdb2e7bdb40fa75.png)
![P(X \in ]x;y])\,=\,P(x < X \le y)\,=\,F_X(y) - F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/9/94ceb8a34851764d5f80ebd0d0594f66_1ebed49db31076c02976044607508915.png)
![P(X \in ]- \infty;x[)\,=\,P(X <x)\,=\,F_X(x_-),](https://static.techno-science.net/illustration/Definitions/autres/e/e0b87b999446176c0481f9c6a2abfa6d_49982d2af2df8b3d5e2ba30bf3689fe9.png)
![P(X \in ]x;y[ )\,=\,P(x < X < y)\,=\,F_X(y_-)-F_X(x),](https://static.techno-science.net/illustration/Definitions/autres/7/7b077fb7ab1e58a23f36381dffdcd06a_9f6abc53e79e20e1f816b453e40843f3.png)
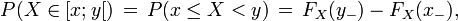
![P(X \in [x;y])\,=\,P(x \le X \le y)\,=\,F_X(y) - F_X(x_-),](https://static.techno-science.net/illustration/Definitions/autres/c/ce63ede7d5a3aaf1e9ef1de86c0f367e_9b1ad3d99926f0a674b14f14d5064bca.png)