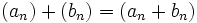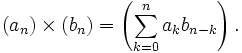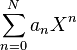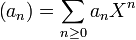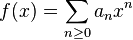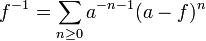Série formelle - Définition

Introduction

En mathématiques, les séries formelles sont un outil qui permet d'utiliser l'arsenal analytique des séries entières sans tenir compte de la notion de convergence. Pour cela on construit une série, non pas comme une fonction à l'aide d'une variable x, mais comme un être algébrique à l'aide d'une indéterminée X. Ces séries sont également très utiles pour décrire de façon concise des suites et pour trouver des formules pour des suites définies par récurrence via ce que l'on appelle les fonctions génératrices.

Considérons un anneau commutatif R. Nous voudrions définir l'anneau des séries formelles sur R de l'indéterminée X, noté R[[X]] ; n'importe quel élément de cet anneau peut être écrit de façon unique comme une somme infinie de la forme ∑_n≥0 a_n Xⁿ où les coefficients a_n sont des éléments de R. En fait, R[[X]] est un anneau topologique et ces sommes infinies sont définies correctement et convergent, non pas au sens d'une fonction mais au sens des séries formelles. L'addition et la multiplication sont les mêmes que pour les séries entières.

Une construction formelle

Considérons l'ensemble R^N de toutes les suites infinies à valeurs dans R et définissons la somme de deux telles suites de la façon suivante :

et leur produit de cette façon :

Le produit est appelé produit de Cauchy de deux suites de coefficients et est une sorte de produit de convolution discret. Ces deux opérations font de R^N un anneau commutatif dont l'élément neutre pour la multiplication est (1,0,0,...). Nous identifierons l'élément a de R à la suite (a,0,0,...) et nous définissons X comme étant égal à (0,1,0,0,...). Alors tout élément de R^N de la forme (a₀, a₁, a₂,...,a_N,0,0,...) peut être écrit comme une somme finie de cette façon :

Afin d'étendre ce développement aux séries infinies, nous avons besoin d'une distance sur R^N : définissons d((a_n), (b_n)) = 2^-k, où k est le plus petit entier naturel tel que a_k ≠ b_k (si un tel k n'existe pas, alors les deux suites seront dites égales et la distance de l'une à l'autre est par conséquent nulle). C'est une distance qui fait de R^N un anneau topologique, et l'expression

peut maintenant être écrite de façon rigoureuse en utilisant la notion de convergence issue de d ; en fait, tout réarrangement de la série converge vers la même limite.

Cet anneau topologique est l'anneau des séries formelles sur R et se note R[[X]].

Les séries formelles vues comme des fonctions

En analyse, une série entière convergente définit une fonction à valeurs réelles ou complexes. Les séries formelles peuvent également être vues comme des fonctions dont les ensembles de départ et d'arrivée sont à manier avec précaution. Si f=∑a_n Xⁿ est un élément de R[[X]], S une algèbre commutative et associative sur R, I un idéal de S tel que la topologie I-adique sur S soit complète, et x un élément de I, alors il est possible de définir :

Cette série converge dans S grâce à l'hypothèse sur x. De plus :

(f + g)(x) = f(x) + g(x)

et

(fg)(x) = f(x)g(x)

Toutefois, ces formules ne sont pas des définitions et doivent être démontrées.

Puisque la topologie sur R[[X]] est la topologie (X)-adique et que R[[X]] est complet, il est possible d'appliquer une série formelle à une autre série formelle, à condition que les arguments n'aient pas de coefficient constant: f(0), f(X²-X) et f( (1-X)^-1 - 1) sont tous bien définis pour toute série formelle f∈R[[X]].

Avec ce formalisme, nous pouvons donner une formule explicite pour l'inverse (au sens multiplicatif) d'une série formelle f dont le coefficient constant a=f(0) est inversible dans R:

Si la série formelle g avec g(0) = 0 est donnée implicitement par l'équation

f(g) = X

où f est une série entière connue vérifiant f(0) = 0, alors les coefficients de g peuvent être calculés explicitement en utilisant le théorème d'inversion de Lagrange.