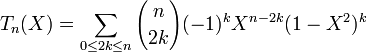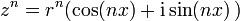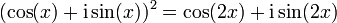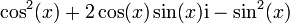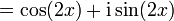Formule de De Moivre - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Utilisations de la formule de De Moivre
Cette formule est utilisée pour rechercher les puissances n-ièmes de nombres complexes sous forme trigonométrique :
ainsi que pour obtenir les formes de cos(nx) et sin(nx) en fonction de sin(x) et cos(x).
Par exemple, pour avoir cos(2x) et sin(2x), on égale :
On a
On identifie les parties réelles et imaginaires :
-
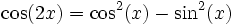
-
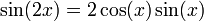
On obtient les formules trigonométriques de duplication.
Polynômes de Tchebychev
La formule de De Moivre donne :
-
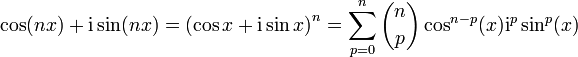
En prenant la partie réelle et en posant p=2k, il vient :
- cos(nx) = Tn(cosx)
où Tn est un polynôme de degré n, appelé polynôme de Tchebychev.
-