Pafnouti Tchebychev - Définition

Introduction

Pafnouti Tchebychev

Pafnouti Lvovitch Tchebychev (en russe : Пафнутий Львович Чебышёв) (16 mai 1821 à Okatovo, près de Borovsk - 8 décembre 1894 à Saint-Pétersbourg) était un mathématicien russe. Son nom est aussi transcrit comme Tschebyscheff (transcription française désuète), Chebyshov ou Chebyshev (forme anglo-saxonne).

Il est connu pour ses travaux dans le domaine des probabilités et des statistiques.

Tchebychev appartient à l'école mathématique russe fondée sous Catherine la Grande par Daniel Bernoulli et Euler. En est aussi issu son contemporain Lobatchevski, initiateur de la géométrie non-euclidienne.

Tchebychev reprend le vaste programme initié par Jacques Bernoulli, Abraham de Moivre et Siméon Denis Poisson pour énoncer et démontrer de façon rigoureuse des théorèmes limites, c'est-à-dire pour établir les tendances asymptotiques des phénomènes naturels. Il établit une loi des grands nombres très générale et donne une nouvelle et brillante méthode de démonstration basée sur l'inégalité démontrée par Bienaymé.

En théorie des nombres, Tchebychev compléta en 1848 une conjecture de Gauss relative à la raréfaction des nombres premiers. Il démontra en 1850 une conjecture énoncée par Bertrand : « Pour tout entier n au moins égal à 2, il existe un nombre premier entre n et 2n ».

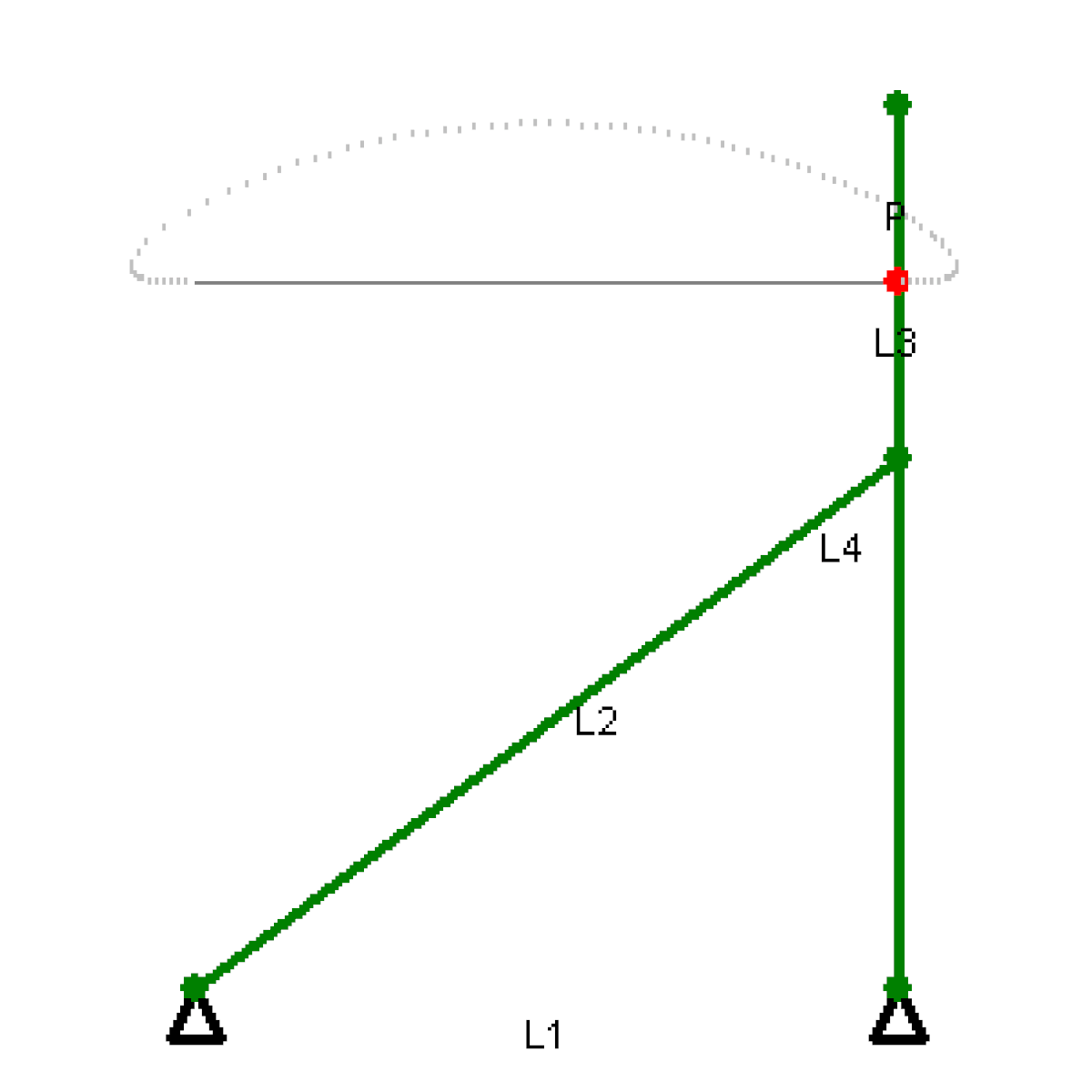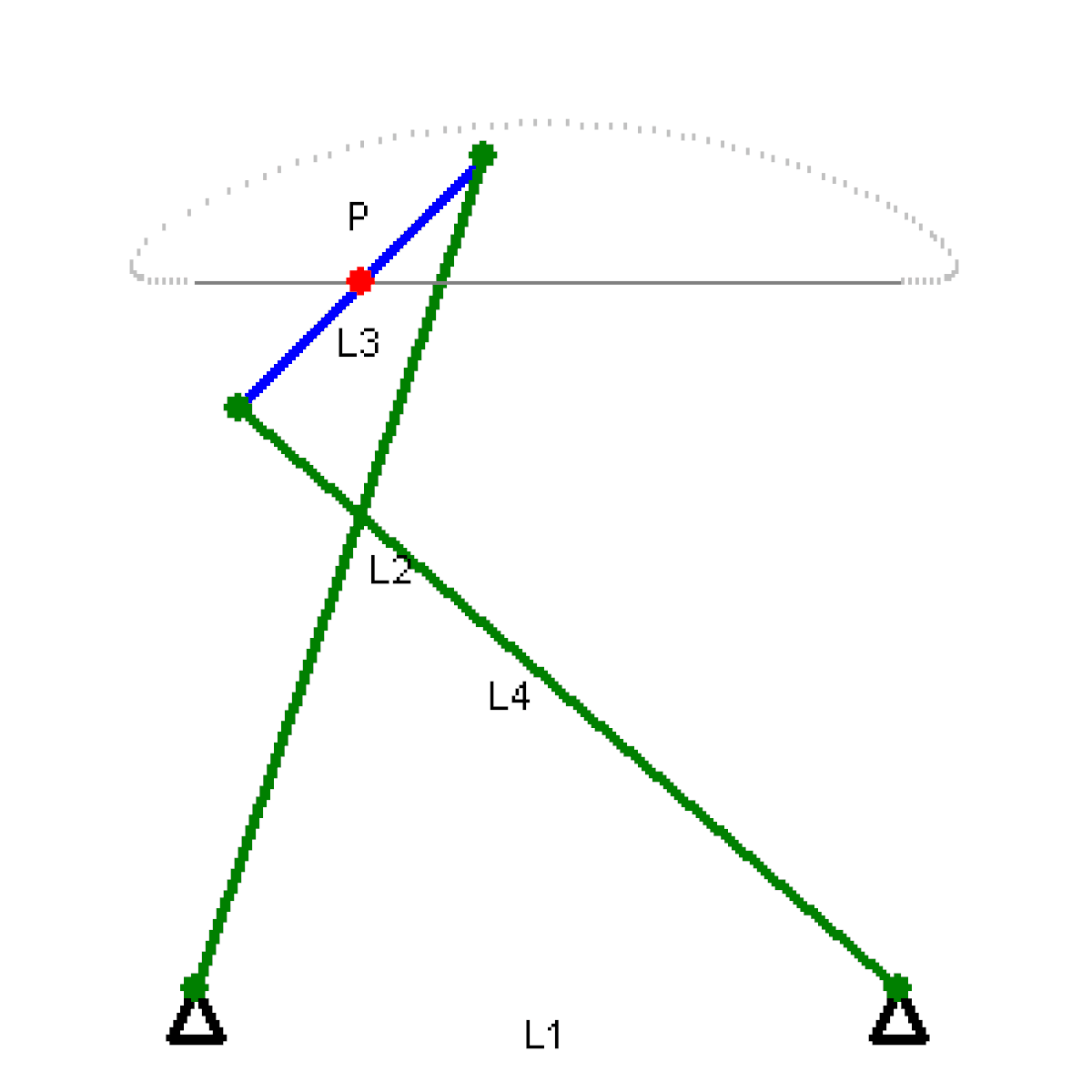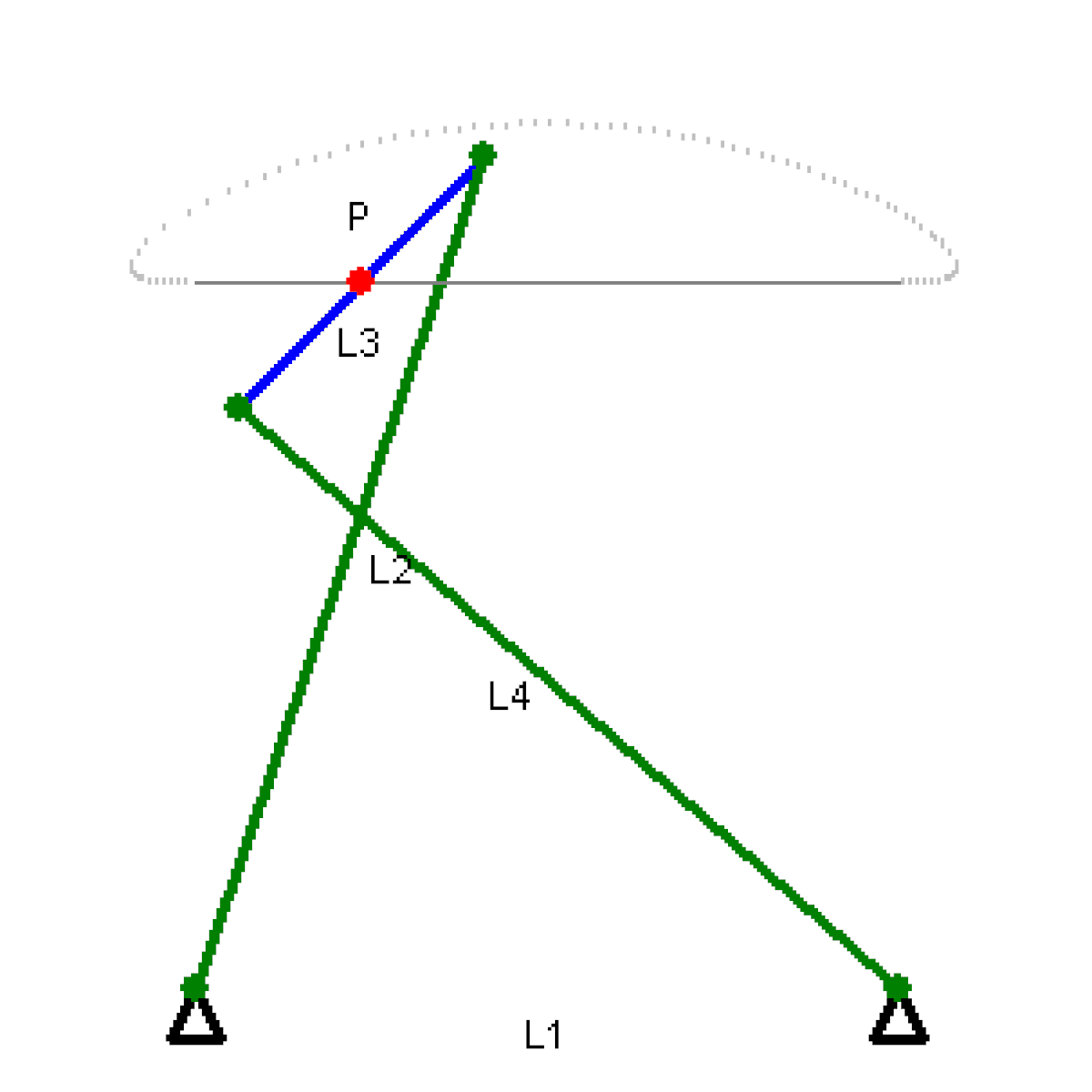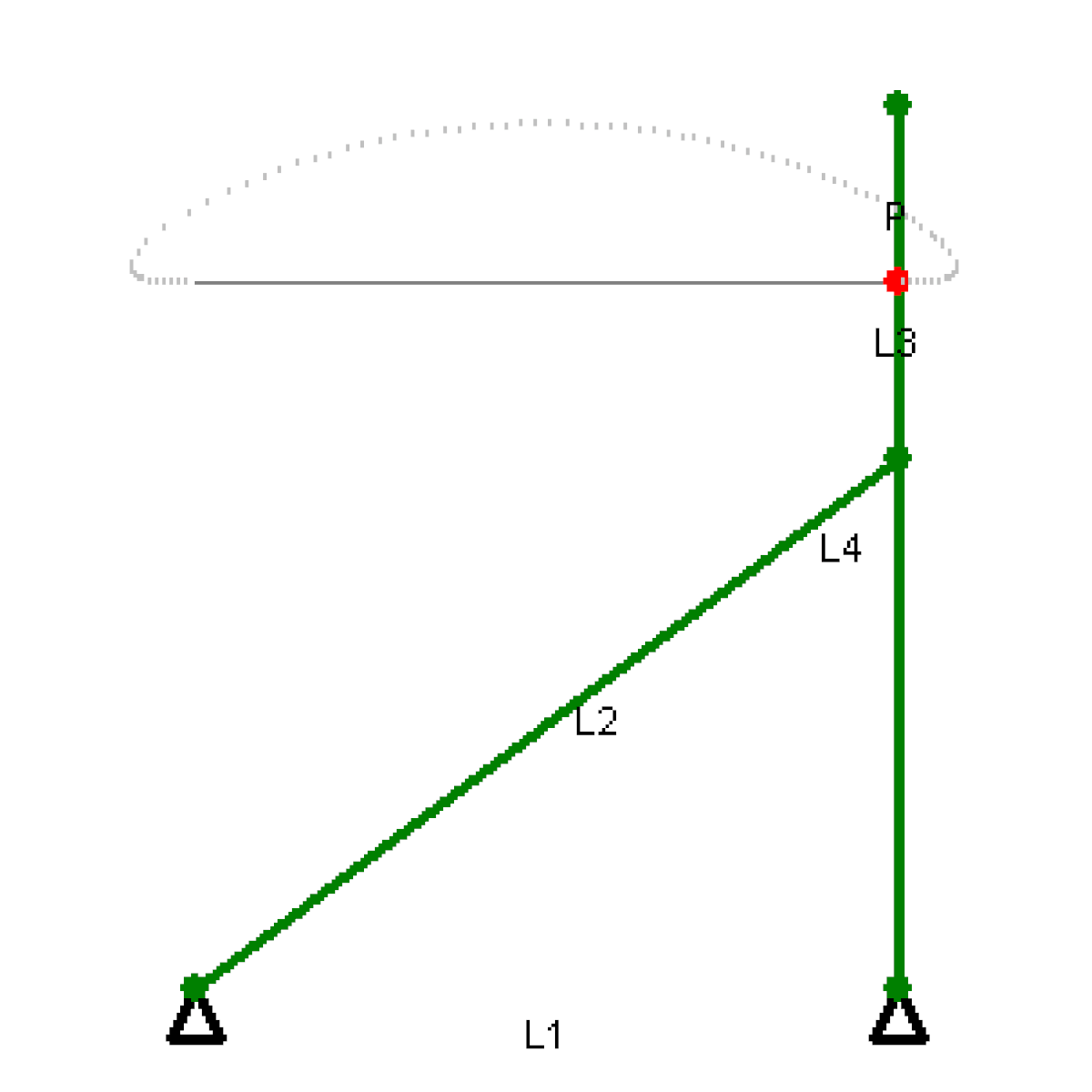
Il a aussi conçu un mécanisme appelé « Cheval de Tchebychev » qui convertit un mouvement de rotation en un mouvement linéaire.

Après lui, Liapounov et Markov, ses élèves, continueront son œuvre et cette tradition russe conduit à Kolmogorov, fondateur des probabilités contemporaines.

• L'inégalité de Tchebychev est utilisée pour prouver la loi faible des grands nombres et le théorème de Bertrand-Tchebychev (1845|1850) mentionné plus haut.
• Les polynômes de Tchebychev sont nommés en son honneur.
• En électronique analogique, il existe une famille de filtres nommée « filtres de Tchebychev ».

Biographie

Pafnouti Lvovitch Tchebychev est né le 16 mai 1821 à Okatovo, une petite ville de l’Ouest de la Russie, à l’ouest de Moscou, dans une famille aisée. Son père est alors officier retraité de l’armée de l’empereur de Russie et a combattu les armées d’invasion napoléoniennes. Tchebychev eut huit frères et sœurs et ses frères suivirent l’enseignement militaire de son père. Lui, pour des raisons médicales, ne pourra pas en faire autant ; en effet, il a une jambe plus courte que l’autre ce qui le handicape et lui interdit l’accès aux armes. Occupant son temps différemment des autres enfants de son âge, il se concentra très tôt sur des activités plus scientifiques et ses capacités intellectuelles furent rapidement remarquées. Sa mère et son cousin prendront en charge dans un premier temps son éducation scolaire, sa mère lui enseignant l’écriture et la lecture quand son cousin lui apprendra le français et l’arithmétique. Plus tard, le français sera pour lui un moyen de communiquer ses travaux mathématiques aux autres scientifiques d’Europe lors des conférences internationales.

En 1832, quand Tchebychev eut 11 ans, la famille déménagea à Moscou. Il eut là-bas un tuteur en mathématiques nommé Pogorelsky, considéré comme le meilleur en la matière du moment. Il fut donc parfaitement préparé à étudier les sciences mathématiques et entra à la prestigieuse université de Moscou en 1837. Là-bas, Tchebychev fut influencé par Nikolaï Dmetrievitch Brashman, alors professeur de mathématiques appliquées depuis 1834, et il fut fasciné par les travaux d’ingénierie mécanique et hydraulique de ce dernier. Brashman apprit à ses élèves les théories d’intégration et des fonctions algébriques ainsi que les calculs de probabilité. En 1841, Tchebychev obtint son premier degré d’études universitaires et continua dans cette même université pour un master, toujours sous l’enseignement de Brashman. Sa première publication, écrite en français, traitait des intégrales multiples. Il l’envoya à Liouville en 1842 et elle apparut dans le journal de Liouville en 1843. Il continua à rechercher la reconnaissance internationale en envoyant au journal de Crelle sa seconde publication dès 1844, toujours écrite en français, cette fois-ci sur les convergences des séries de Taylor. À l’été 1846, il soutint sa thèse. La même année, le journal de Crelle édita une nouvelle publication de Tchebychev sur cette thèse, où il poursuivait le programme de Bernouilli et de Poisson consistant à donner un cadre théorique aux théorèmes limites des probabilités, en développant des résultats rigoureux mais élémentaires. En 1847, il fut invité à présenter sa thèse à Saint-Pétersbourg : l’intégration au moyen des logarithmes. Il écrivit un livre intitulé teoria sravneny présentant des travaux relatifs à la théorie des nombres, qui parut en 1849 et qui lui servit à soutenir son doctorat cette même année. Cependant cette thèse ne fut publiée qu’après sa mort, il se contenta de publier quelques-uns de ces résultats en 1853.

Tchebychev fut promu professeur extraordinaire à Saint-Pétersbourg en 1850. Deux ans après, il entreprit des voyages en France, en Angleterre et en Allemagne. Là-bas, il s’entretint avec de grands mathématiciens dont le français Bienaymé. Ces rencontres furent un tournant dans sa vie qui le conduisit à se lancer dans des recherches sur les théories des mécanismes et les théories des approximations, d’où il tira les grandes lois qui portent aujourd’hui son nom. On peut citer par exemple les polynômes de Tchebychev, les filtres de Tchebychev ou encore l'inégalité de Bienaymé-Tchebychev qui seront exposés dans le chapitre suivant. Il créa des liens avec des savants occidentaux et retourna régulièrement en France de 1873 jusqu’à 1893 où il tint une demi-dizaine de conférences dans les principales villes du pays. En 1893, à l’exposition universelle de Chicago, il exposa sept de ses inventions, dont une bicyclette spéciale pour femme. Il prit sa retraite du professorat de l’université de Saint-Pétersbourg en 1892. On peut noter que pendant sa carrière, il reçut un nombre important de distinctions honorifiques de la part de la ville où il enseignait : il fut dès son jeune âge académicien junior de l’Académie des sciences de Saint-Pétersbourg (1853), puis académicien extraordinaire (1856) et enfin académicien (1859). Il fut également un grand correspondant de la Russie auprès de plusieurs académies d’Europe occidentale : Liège (1856), Berlin (1871), Bologne (1873), Paris (1874), Londres (1877), Italie (1880) et Stockholm (1893) ; il reçut la Légion d’honneur en récompense de ses travaux en coopération avec les grands mathématiciens français de son temps. La mort l’emporta le 8 décembre 1894 à Moscou.

Sur sa vie personnelle, on sait qu’il ne s’est jamais marié et qu’il a toujours habité seul dans une grande maison, richement décorée. Il eut une fille, mais ne la reconnut jamais officiellement. Elle fut élevée par la sœur de Tchebychev et ce dernier l’aida financièrement même après son mariage avec un colonel.