Courbe algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie algébrique, une courbe est une variété algébrique (ou un schéma de type fini) sur un corps, dont les composantes irréductibles sont de dimension 1. En dehors des variétés algébriques de dimension 0 qui se réduisent aux algèbres finies sur un corps, les courbes sont les premières variétés algébriques non triviales.
Définition
Sous sa forme la plus générale, une courbe algébrique sur un corps k est une variété algébrique de dimension 1 sur k, séparée pour éviter des pathologies. En considérant les composantes irréductibles munies de la structure réduite, on se ramène aux courbes intègres. Par compactification et normalisation, on se ramène aux courbes projectives régulières, ce qui est la situation le plus couramment abordée.
Exemples.
- La droite affine
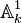
- La droite projective
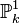
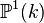
- Courbe plane affine: c'est une sous-variété fermée du plan affine
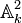
![F(x,y)\in k[x,y]](https://static.techno-science.net/illustration/Definitions/autres/2/264e3477c8b72067c1dd9e207c779574_c595b4f0b7a5bc3faffe76a62afa05e5.png)
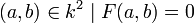
- C'est en quelque sorte la forme historique des courbes algébriques au moins lorsque le corps de base est

- Courbe plane projective: c'est une sous-variété fermée du plan projectif
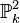
![F(x,y,z)\in k[x,y,z]](https://static.techno-science.net/illustration/Definitions/autres/a/a7806d7032e368274cd5cef9ce7b1367_c28b19c08bfd8133a916648c3b7de100.png)
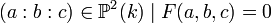
- Les courbes elliptiques et les courbes de Fermat xn + yn − zn = 0 sont des courbes projectives planes.
Dans toute la suite, sauf dans la dernière section, on se placera dans le cadre des courbes projectives irréductibles et lisses C sur un corps k. On sait que cela implique que C est régulière. Pour simplifier on suppose de plus que OC(C) = k (donc C reste irréductible sur la clôture algébrique de k).
Diviseurs
Un diviseur sur C est une somme (formelle) finie
| D = | ∑ | ax[x] |
| x |
à coefficients ax entiers, indexée par des points (fermés) x de C. Les ax sont tous nuls sauf pour un nombre fini d'entre eux. Le coefficient ax se note aussi vx(D). C'est la valuation de D en x. L'ensemble des diviseurs forment un groupe abélien libre Z1(C) dont une base est constituée des classes [x],
On définit le degré de D par
| deg(D) = | ∑ | ax[k(x):k] |
| x |
où k(x) est le corps résiduel en xi, extension finie de k par le théorème des zéros de Hilbert. L'application degré est un morphisme de groupes
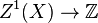
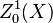
Il y a un type particulièrement important de diviseurs, les diviseurs principaux. Il s'agit des diviseurs (f) associés aux fonctions rationnelles non nulles
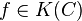
| (f) = | ∑ | ordx(f)[x], |
| x |
où ordx(f) est l'ordre d'annulation de f en x si f est régulière en x, et c'est l'opposé de son ordre de pôle sinon.
On montre que tout diviseur principal est de degré 0. L'ensemble des diviseurs principaux forment un sous-groupe du groupe
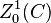
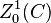
On dit que deux diviseurs sur C sont linéairement équivalents s'ils diffèrent par un diviseur principal.
Si D est un diviseur, on lui associe un faisceau inversible OC(D) sur C de la manière suivante: pour tout ouvert affine U de C, OC(D)(U) est égal à l'union de 0 avec l'ensemble des fonctions rationnelles non-nulles f vérifiant
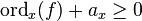
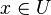
Inversement, tout faisceau inversible est isomorphe à un OC(D), D étant unique à équivalence linéaire près.
- Diviseur canonique Le faisceau des formes différentielles ΩC / k sur C est un faisceau inversible. C'est le fibré cotangent sur C. Il lui correspond donc un diviseur K, unique à équivalence linéaire près. Un tel diviseur est appelé un diviseur canonique de C.

















































