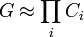Groupe abélien fini - Définition

Propriétés

Propriétés élémentaires

• Tout groupe cyclique est abélien (donc tout groupe cyclique fini est un groupe abélien fini).
• Tout sous-groupe d'un groupe abélien fini est abélien et fini.
• Tout groupe quotient d'un groupe abélien fini est abélien et fini.
• Tout produit direct d'une famille finie de groupes abéliens finis est un groupe abélien fini.

La première propriété est démontrée dans le paragraphe Théorème fondamental de l'article groupe cyclique, les autres sont le propre des groupes abéliens et des groupes finis.

Théorème de Kronecker

Dans le reste de l'article, G désigne un groupe abélien fini :

• Il existe une suite d'entiers strictement positifs (a₁,a₂,...,a_k) tel que G est isomorphe au produit direct des groupes cycliques de cardinal les différents éléments de la suite.

Il existe donc la suite suivante isomorphe au groupe G:

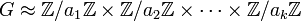
• Si la suite (a₁,a₂,...,a_k) est choisie de tel sorte que a_i+1 divise a_i pour tout i entier entre 1 et k - 1, alors la suite est unique. Les éléments de cette suite sont appelés facteurs invariants.

Ce théorème est démontré dans l'article détaillé.

Conséquences du théorème de Kronecker

La définition suivante permet d'obtenir une autre décomposition :

• Soit p un nombre premier, un groupe abélien est dit de p-torsion si tous ses éléments sont d'ordre une puissance de p.

Dans le cas des groupes finis un groupe de p-torsion correspond exactement à la notion de p-groupe.

• Il existe une et une unique décomposition de G en produit de groupes de p_i-torsions fini, à l'ordre près. Ici (p_i) désigne une famille de nombres premiers.

Il existe aussi une autre décomposition plus fine :

• Il existe une unique décomposition de G en produit de cycles d'ordre une puissance d'un nombre premier.

On dispose de plus, de la propriété suivante :

• Soit d un diviseur de l'ordre de G, il existe un sous-groupe de G d'ordre d.

• Il existe une et une unique décomposition de G en produit de groupes de p_i-torsions fini, à l'ordre près.

Existence

Le théorème de Kronecker limite la démonstration au cas d'un groupe cyclique. En effet, comme tout groupe abélien fini est un produit de groupes cycliques, et que le produit direct d'un nombre fini de p-groupes est un p-groupe, il suffit alors de regrouper tous les p-groupes obtenus.

Le théorème chinois indique que si a et b sont deux entiers premiers entre eux alors Z/ab.Z est isomorphe à Z/a.Z x Z/b.Z. Il permet de conclure.

Unicité

Il suffit pour cela de remarquer que le p_i-groupe est formé des éléments dont l'ordre est une puissance de p_i.

• Il existe une unique décomposition de G en produit de cycles d'ordre une puissance d'un nombre premier.

La proposition précédente limite la démonstration à l'existence et l'unicité d'une décomposition en produit direct de cycles pour un p-groupe.

L'existence est une conséquence directe du théorème de Kronecker.

L'unicité se démontre par récurrence.

Si le p-groupe est de cardinal p, alors il n'admet pas de sous-groupe et sa décomposition est unique.

Supposons la démonstration établie à l'ordre p^k, montrons qu'elle est aussi vraie à l'ordre p^{k + 1}. Soit p^l l'exposant du p-groupe, toute décomposition en produit de cycle contient au moins un groupe cyclique d'ordre p^l et ne contient aucun cycle d'ordre p^m avec m > l (sinon l'exposant serait égal à p^m). La démonstration du théorème de Kronecker montre qu'il existe une unique décomposition du p-groupe en un groupe cyclique d'ordre p^l et d'un sous-groupe G'. L'hypothèse de récurrence montre l'unicité de la décomposition du groupe G' et termine la démonstration.

• Il existe un sous-groupe de G d'ordre d.

Soit g l'ordre du groupe G, le théorème de Kronecker indique qu'il existe un isomorphisme entre G et un produit de cycles :

soit c_i l'ordre de C_i, le produit des c_i est égal à g, donc il existe une famille d'entiers d_i tel que d_i divise c_i et que le produit des d_i soit égal à d. Il existe un sous-groupe D_i de C_i d'ordre d_i (cf troisième proposition du paragraphe Théorème fondamental de l'article Groupe cyclique). Le produit des sous-groupes D_i est isomorphe à un sous-groupe de G d'ordre d.