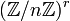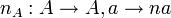Variété abélienne - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définition - Isogénie - Propriétés basiques - Module de Tate - Anneaux d'endomorphismes - Polarisation - Variété abélienne duale

Introduction

En mathématiques, et en particulier, en géométrie algébrique, une variété abélienne A est, grosso modo, un groupe algébrique projectif. La projectivité (l'équivalent de compacité pour les variétés différentielles ou analytiques) donne une certaine rigidité à la structure. En géométrie arithmétique, c'est un objet central.

Définition

Une variété abélienne sur un corps k est un groupe algébrique A sur k, dont la variété algébrique sous-jacente est projective, connexe et géométriquement réduite. Cette dernière condition veut dire que lorsque l'on étend le corps de base k à une clôture algébrique de k, la nouvelle variété est réduite (cela implique que A est réduite). Si k est de caractéristique nulle, la condition "géométriquement réduite" est automatiquement satisfaite pour tout groupe algébrique sur k (Théorème de Cartier).

Exemple: Les variétés abéliennes de dimension 1 sont les courbes elliptiques.

La jacobienne d'une courbe algébrique projective non-singulière géométriquement connexe, de genre g, est une variété abélienne de dimension g.

Si A est une variété abélienne de dimension $g$ sur ℂ, alors A(ℂ) est naturellement une variété analytique complexe, et même un groupe de Lie. C'est le quotient (au sens de la géométrie analytique complexe) de ℂ $g$ par un réseau $Λ$ , le quotient admettant un plongement dans un espace projectif.

Isogénie

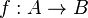
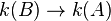
Un homomorphisme $f : A \to B$ de variétés abéliennes est une isogénie si A et B ont la même dimension et si le noyau de f est fini. Ce dernier est alors le spectre d'une algèbre finie sur $k$ , dont la dimension vectorielle est appelée le degré de $f$ . C'est aussi le degré de l'extension des corps de fonctions rationnelles $k(B) \to k(A)$ induite par $f$ .

Un exemple typique d'isogénie est la multiplication par n :

pour tout entier naturel n (même quand il est divisible par la caractéristique de k). Cette isogénie est de degré $n 2 g$ si $g = dim A$ .

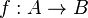
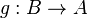
Théorème Si $f : A \to B$ est une isogénie, alors il existe une isogénie $g: B \to A$ telle que $f g = n B$ et $g f = n A$ .

On dit que $A$ est simple si elle n'a pas d'autres sous-variété abélienne que {0} et elle-même. Par exemple toute courbe elliptique est simple, mais pas le produit de deux courbes elliptiques. On dit que $A$ est absolument simplet si elle est simple sur une clôture algébrique de $k$ .

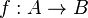
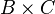
Théorème (irréductibilité complète de Poincaré) Si $f : A \to B$ est un homomorphisme de variétés abéliennes surjectif, alors il existe une sous-variété abélienne C de A telle que A soit isogène à $B \times C$ .

On en déduit que toute variété abelienne A est isogène à un produit de variétés abeliennes simples. L'ensemble de ces facteurs simples est unique à permutations et isogénies près.

Propriétés basiques

Une variété abélienne $A$ est toujours non-singulière, et la loi de groupe sur $A$ est commutative.

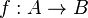
Si $A$ et $B$ sont des variétés abéliennes sur $k$ , et si $f : A\to B$ est un morphisme de variétés algébriques qui envoie le zéro de $A$ sur le zéro de $B$ , alors $f$ est un hommorphisme de groupes algébriques (c'est-à-dire que $f$ est compatible avec les structures de groupes algébriques sur $A$ et $B$ ).

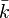
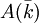
Structure de la torsion Si A est une variété abélienne de dimension g définie sur un corps k et si n est un entier naturel premier à la caractéristique de k, alors l'ensemble $A(\bar{k})[n]$ des éléments de A à coordonnées dans une clôture algébrique $\bar{k}$ de k et qui sont d'ordre divisant n (c'est donc le noyau de l'application multiplication par n dans le groupe $A(\bar{k})$ ) est un groupe fini, isomorphe à $(\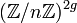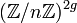mathbb{Z}/n\mathbb{Z})^{2g}$ . En particulier, les points de $A$ à coordonnées dans $k$ et qui sont d'ordre divisant $n$ est un sous-groupe de $(\mathbb{Z}/n\mathbb{Z})^{2g}$ .

Si $k$ est de caractéristique $p > 0$ , alors il existe un entier $r$ compris entre 0 et $g$ tel que pour toute puissance $n$ de $p$ , $A(\bar{k})[n]$ soit isomorphe à $(\mathbb{Z}/n\mathbb{Z})^{r}$ . On appelle $r$ le $p$ -rang de $A$ . On dit que $A$ est ordinaire si son $p$ -rang prend la valeur maximale, c'est-à-dire $g$ .