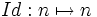Application identique - Définition

En mathématiques, une application identique ou fonction identique f est une application qui n'a aucun effet lorsqu'elle est appliquée à un élément : elle renvoie toujours la valeur qui est utilisée comme argument, c'est-à-dire qu'on a toujours f(x) = x.

Formellement, si M est un ensemble, nous définissons l'application identique id_M sur M et d'ensemble d'arrivée M et qui satisfait :

pour tout élément x dans M, id_M(x) = x

Si f : M → N est une application quelconque, alors nous avons f o id_M = f = id_N o f. En particulier, id_M est l'élément neutre du monoïde de toutes les fonctions de M vers M.

Lorsque nous choisissons M égal à l'ensemble des entiers naturels non nuls, nous obtenons l'application identique , qui est une fonction multiplicative considérée en théorie des nombres.