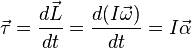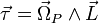Gyroscope - Définition

Lois physiques

Exemple de mouvement de précession de l'axe d'un gyroscope.

L'équation fondamentale décrivant le comportement du gyroscope est :

où les vecteurs et sont respectivement le moment (ou couple) sur le gyroscope et son moment cinétique, le scalaire I est son moment d'inertie, le vecteur est sa vitesse angulaire, et le vecteur est son accélération angulaire.

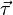
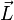
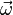
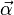
Il découle de cela qu'un moment appliqué perpendiculairement à l'axe de rotation, et donc perpendiculaire à , provoque un déplacement perpendiculaire à la fois à et . Ce mouvement est appelé précession. La vitesse angulaire de la précession Ω est donnée par

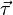
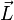
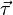
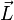
Le phénomène de précession peut être observé en plaçant un gyroscope tournant autour de son axe vertical et soutenu par le sol ou un point fixé au sol à une extrémité. Au lieu de tomber comme on peut s'y attendre, le gyroscope apparaît comme défiant la gravité en restant sur son axe vertical, même si un bout de l'axe n'est pas soutenu. L'extrémité libre de l'axe décrit lentement un cercle dans un plan horizontal. Les équations précédentes décrivent cet effet. Le moment du gyroscope est fourni par un couple de forces : la gravité pousse vers le bas le centre de la masse du dispositif, et une force égale la pousse vers le haut pour soutenir le côté libre. Le déplacement résultant de ce moment n'est pas vers le bas, comme l'intuition nous le fait supposer, mais perpendiculaire à la fois au mouvement gravitationnel (le bas) et l'axe de rotation (vers l'extérieur du point d'appui), c'est-à-dire dans une direction horizontale vers l'avant, faisant faire à l'appareil une rotation lente autour du point de support.

Comme démontre la deuxième équation, sous un moment constant dû à la gravité, la vitesse de précession du gyroscope est inversement proportionnelle à son moment cinétique. Cela signifie que, comme la friction fait ralentir le mouvement tournant du gyroscope, le taux de précession augmente. Cela continue jusqu'à ce que le dispositif ne puisse plus tourner suffisamment rapidement pour soutenir son propre poids, alors il arrête la précession et tombe hors de son support.