Homotopie - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Convexe d'un espace euclidien
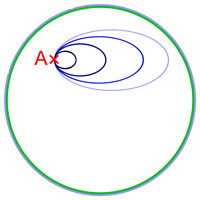
Soit E un espace euclidien de dimension n, où n est un entier strictement positif. On dispose de la propriété suivante :
-
- Tout lacet d'ensemble convexe C non vide de E est homotope à un point, c'est-à-dire à un lacet constant.
La figure de droite illustre le cas d'un lacet dans un disque. Ce lacet est manifestement homotope à un point, c'est-à-dire homotope à un lacet constant. Autrement dit, un convexe d'un espace euclidien (plus généralement d'un espace vectoriel topologique localement convexe) est simplement connexe.
Soit A est un élément de C, l'objectif est de montrer que tout lacet γ basé en A (c'est-à-dire ayant pour origine et extrémité A), est homotope au point A. Pour cela on définit une application H : [0 1]2 → C définie par :
![\forall t,s \in [0,1]\quad H(t,s)= tA + (1-t)\gamma(s)](https://static.techno-science.net/illustration/Definitions/autres/f/f92b49fadc85b364526de613f8d3988a_f858095ab0160c7f65c1f60d2a1e06e1.png)
L'application H est manifestement continue, comme γ(x) et A sont deux éléments de C, pour toutes valeurs de t et de s H(t, s) est élément de C car C est convexe. L'application H définit bien une homotopie entre le lacet constant et γ.
Cercle
Dans le cas d'un cercle C, identifié ici aux complexes de module 1, la situation n'est pas équivalente à la précédente. Intuitivement, si un fil parcourt une boucle autour d'un cercle, il n'est pas possible de le ramener à un point sans que le fil ne quitte la surface du cercle et sans le briser. On définit le lacet α comme l'application de [0, 1] dans C, qui à t associe exp(2πi.t) et c le lacet constant qui à t associe 1.
On dispose de la propriété :
-
- Le lacet du cercle α n'est pas homotope à c.
Cette vérité est en général démontrée dans un résultat plus large, établissant la structure du groupe fondamental du cercle, on peut néanmoins procéder plus directement ici. Intuitivement, si le lacet s'imagine comme un fil qui tourne autour du cercle, tirer suffisamment fort sur les deux brins que l'on trouve au point 1 pour ramener l'intégralité du fil en 1, va casser le fil. Trouver le point de cassure est une méthode pour exhiber une discontinuité.
On raisonne par l'absurde.
- Soit H(t, s) une homotopie stricte du lacet α vers c.
- Pour une valeur de s donnée, la fonction t → H(t, s) n'est pas toujours surjective, par exemple pour s égal à 1, elle ne l'est pas car elle est constante. Soit N l'ensemble des points s de[0, 1] tel que t → H(t, s) ne soit pas surjectif. Cet ensemble ne contient pas 0, et est ouvert. En effet, si s est élément de N, il existe un point z de du cercle, qui n'est pas atteint par H(., s). L'image de H(., s) est un compact, car H est continue et H(., s) est définie sur un compact. Le complémentaire est ouvert donc z est élément d'un ouvert ne rencontrant pas l'image de H(., s). L'uniforme continuité de H, garantie par le fait que H est continue et définie sur un compact, montre qu'il existe un voisinage de s tel que l'image de H(., s) ne rencontre pas z. Soit s0 la borne inférieure de la composante connexe de N contenant 1. Cette borne inférieure est au moins égal à 0, strictement inférieure à 1 et ne fait pas partie de N, car N est ouvert.
Un instant s0 où se produit une déchirure est maintenant connu, il s'agit de trouver le point H(t0, s0), indiquant l'endroit où se produit cette déchirure pour trouver une discontinuité.
- Pour s élément de ]s0, 1], on définit Ns comme l'adhérence union des images suivantes :
![\mathcal N_s = \overline {\bigcup_{s_0<\sigma<s} \Big\{z \in \mathcal C,\; \forall t \in [0,1]\quad H(t,\sigma) \neq z\Big\}}](https://static.techno-science.net/illustration/Definitions/autres/c/cd30ac7abc22c08d5f0273b7b2583e7d_0e7911f35b24e82c33a1bbc24c26585b.png)
- Soit z0 un élément de l'intersection IN des Ns, lorsque s décrit ]s0, 1]. Comme ces Ns forment un ensemble de fermés emboîtés non vides dans le compact C, l'intersection n'est pas vide et z0 existe bien. Comme s0 n'est pas élément de N, la fonction H(.,s0) est surjective et il existe un élément t0 tel que H(t0, s0) est égal à z0. le point de déchirure (t0, s0) est maintenant trouvé.
Il faut encore montrer que le point de déchirure est bien une discontinuité de H.
- On considère les deux points du cercle situés à une distance de 1/2 de z0 et t1, t2 leurs antécédents par la fonction qui à t associe H(t, s0). Comme H(., s0) est une fonction surjective, les deux valeurs existent bien. Comme la fonction H est uniformément continue, il existe un réel strictement positif δ, plus petit que 1 - s0 tel que :
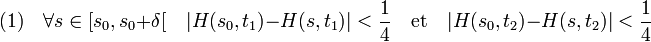
- Comme z0 est adhérent à l'ensemble IN il existe une valeur z à une distance strictement inférieure à 1/4 de z0 et une valeur σ de l'intervalle ]s0, s0 + δ[, tel que H(., σ) ne contienne pas z dans son image. L'image de l'intervalle [t1, t2] par la fonction H(., σ) ne contient ni z ni -z, d'après la propriété (1). Sans ces deux points, le cercle contient au moins deux composantes connexes. Les points H(σ, t1) et H(σ, t2) sont dans deux composantes connexes distinctes. En conséquence, l'image de l'intervalle [t1, t2] par H(σ, .) n'est pas connexe, ce qui montre que H ne peut pas être continu.

















































