Idéal - Définition

Idéaux particuliers

Idéal maximal : un idéal M est maximal s'il existe exactement deux idéaux contenant M, à savoir A et M lui même, autrement dit si A/M est un corps.

Idéal premier : dans un anneau commutatif unitaire, un idéal I est premier si I est différent de A, et pour tous a et bde A tels que , on a la propriété que si alors . Ainsi, I est premier si et seulement si A/I est intègre.

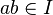
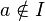
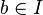
Idéal irréductible : dans un anneau commutatif unitaire, un idéal I est irréductible s'il ne peut pas s'écrire comme intersection de deux idéaux différents de I.

(Dans un anneau commutatif unitaire, tout idéal maximal est premier et tout idéal premier est irréductible.)

Idéal principal : l'idéal engendré par un élément a de l'anneau est par définition le plus petit idéal contenant a. On le note (a). Un idéal I d'un anneau A est principal s'il existe un élément a de A tel que I=(a).

Un anneau intègre dont tous les idéaux sont principaux est dit anneau principal. Par exemple, ou l'anneau K[X] des polynômes sur un corps K sont des anneaux principaux.

Idéal de type fini : c'est un idéal engendré par un nombre fini d'éléments . Donc tout élément de l'idéal s'écrit comme avec des (s'il s'agit d'un idéal à gauche).

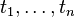
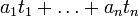
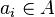
Idéal radiciel : un idéal est radiciel s'il est égal à son radical . C'est le cas par exemple de tout idéal premier dans un anneau commutatif unitaire.

Idéal primaire : dans un anneau commutatif unitaire, un idéal I est primaire si pour tous a et b de A tels que , si alors, il existe un entier naturel n tel que .

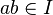
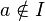
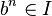
Idéal décomposable : dans un anneau commutatif unitaire, un idéal est décomposable s'il est l'intersection finie d'idéaux primaires.