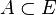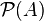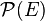Idéal - Définition
La liste des auteurs de cet article est disponible ici.
Définition
Une partie I d'un anneau A est un idéal à gauche de A si :
- I est un sous-groupe additif de A.
-
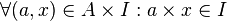
Le produit, à gauche, d'un élément de I par un élément de A appartient à I.
et est un idéal à droite de A si :
- I est un sous-groupe additif de A.
-
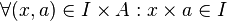
Le produit, à droite, d'un élément de I par un élément de A appartient à I.
Un idéal bilatère est un idéal à gauche et à droite. Dans un anneau commutatif, les notions d'idéal à droite, d'idéal à gauche et d'idéal bilatère se confondent et on parle alors simplement d'idéal.
Exemples:
- Pour tout entier relatif k,
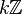

- Si A est un anneau, {0} et A sont des idéaux triviaux de A. Ces idéaux sont sans intérêt, c'est la raison pour laquelle on appellera idéal propre un idéal différent de A.
- Si A est un anneau unitaire et si I est un idéal contenant 1 alors I = A. Plus généralement, si I contient un élément inversible alors I = A
- Les seuls idéaux dans un corps K sont les idéaux triviaux ; c'est pourquoi le domaine d'application des idéaux est la divisibilité dans un anneau.
Radical d'un idéal d'un anneau commutatif
Si I est un idéal d'un anneau commutatif A, on appelle radical de I, noté
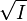
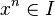
- Exemple:
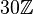
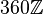
Si A est un anneau commutatif, on a les propriétés suivantes
-
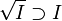
-
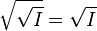
-
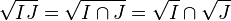
-
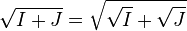
- Si de plus A est unitaire,
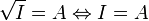
Opérations portant sur les idéaux
Dans ce qui suit, on suppose que les idéaux considérés sont de même type (par ex. tous bilatères)
Somme : si I et J sont deux idéaux d'un anneau alors l'ensemble
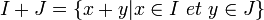
Intersection : une intersection quelconque d'idéaux reste un idéal.
L'ensemble des idéaux de A muni de ces deux opérations forme alors un treillis.
Idéal engendré : la seconde loi permet de mettre en place cette notion. Si P est une partie d'un anneau , on appelle idéal engendré par P l'intersection de tous les idéaux de A contenant P.
- Exemples:
-
- Pour un anneau commutatif A et un élément a de cet anneau, l'idéal engendré par {a} est aA (par exemple l'idéal de
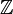
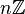
- Pour I et J deux idéaux de A, le sous-ensemble
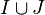
- Pour un anneau commutatif A et un élément a de cet anneau, l'idéal engendré par {a} est aA (par exemple l'idéal de
-
Produit : si I et J sont deux idéaux bilatères d'un anneau, on appelle produit de I et J l'idéal IJ égal à l'ensemble des sommes finies
| ∑ | xkyk |
| k |
où
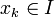
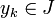
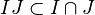
- Exemple : dans l'anneau
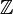
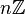
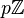
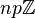
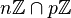
Anneau quotient : si I est un idéal bilatère, la relation
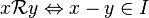
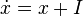
- Article détaillé : Anneau quotient
Autres types d'idéaux
Idéal fractionnaire
Si A est un anneau commutatif intègre et si K est son corps des fractions, un idéal fractionnaire de A est une partie de K de la forme d-1J où d est un élément non nul de A et J un idéal de A. (Attention à cette appellation trompeuse : un idéal fractionnaire de A n'est en général pas un idéal de A, ni même une partie de A.)
- Exemple : si A est l'anneau Z des entiers, son corps des fractions est le corps Q des rationnels. Si n et d sont deux entiers, avec d non nul, l'ensemble (d -1)(n Z) des rationnels qui peuvent s'écrire
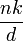
Sur l'ensemble des idéaux fractionnaires, on peut définir des intersections, des sommes et des produits. Un idéal fractionnaire I est dit inversible s'il existe un idéal fractionnaire L tel que I.L = A.
Un cas particulier important est celui où A est un anneau d'entiers algébriques d'une extension finie du corps Q. On arrive alors à montrer que l'ensemble des idéaux fractionnaires est un groupe pour l'opération produit. Il est intéressant de considérer le groupe quotient des idéaux fractionnaires modulo les idéaux principaux ; on obtient ainsi une mesure du défaut de principalité, par le groupe des classes d'idéaux. Un théorème affirme que ce groupe est fini.
Idéal d'un treillis
Si T est un treillis, I est un idéal de T ssi I est stable pour la loi
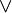

- Exemple : Si E est un ensemble et