Inférence bayésienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
On nomme inférence bayésienne la démarche logique permettant de calculer ou réviser la probabilité d'une hypothèse. Cette démarche est régie par l'utilisation de règles strictes de combinaison des probabilités, desquelles dérive le théorème de Bayes. Dans la perspective bayésienne, une probabilité n'est pas interprétée comme le passage à la limite d'une fréquence, mais plutôt comme la traduction numérique d'un état de connaissance (le degré de confiance accordé à une hypothèse, par exemple ; voir théorème de Cox-Jaynes).
Jaynes utilisait à ce sujet avec ses étudiants la métaphore d'un robot à logique inductive. On trouvera un lien vers un de ses écrits dans l'article Intelligence artificielle.
La manipulation des probabilités : notation et règles logiques
L'inférence bayésienne est fondée sur la manipulation d'énoncés probabilistes. Ces énoncés doivent être clairs et concis afin d'éviter toute confusion. L'inférence bayésienne est particulièrement utile dans les problèmes d'induction. Les méthodes bayésiennes se distinguent des méthodes dites standard par l'application systématique de règles formelles de transformation des probabilités. Avant de passer à la description de ces règles, familiarisons-nous avec la notation employée.
Notation des probabilités
Prenons l'exemple d'une femme cherchant à savoir si elle est enceinte. On définira d'abord une hypothèse E : elle est enceinte, dont on cherche la probabilité p(E). Le calcul de cette probabilité passe évidemment par l'analyse du test de grossesse. Supposons que des études aient démontré que pour des femmes enceintes, le test indique positif 9 fois sur 10. Pour les femmes non-enceintes, le test indique négatif dans un ratio de 19/20. Si l'on définit les hypothèses :
- TP : le test est positif,
- TN : le test est négatif,
on peut interpréter les résultats précédents de manière probabiliste :
La probabilité de l'hypothèse TP sachant que la femme est enceinte est de 0,9.
En langage des probabilités, cet énoncé sera décrit par l'expression p(TP | E) = 0,9. De la même manière
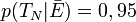
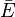
En plus de l'opérateur conditionnel |, les opérateurs logiques ET et OU ont leur notation particulière. Ainsi, la probabilité simultanée de deux hypothèses est notée par le signe
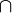
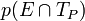
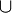
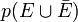
Les règles de la logique des probabilités
Il existe seulement deux règles pour combiner les probabilités, et à partir desquelles est bâtie toute la théorie de l'analyse bayésienne. Ces règles sont les règles d'addition et de multiplication.
La règle d'addition
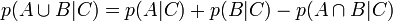
La règle de multiplication
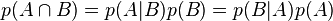
Le théorème de Bayes peut être dérivé simplement en mettant à profit la symétrie de la règle de multiplication
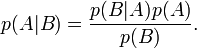
Le théorème de Bayes permet d'inverser les probabilités. C'est-à-dire que si l'on connaît les conséquences d'une cause, l'observation des effets permet de remonter aux causes.
Dans le cas précédent de la femme enceinte, sachant le résultat du test, il est possible de calculer la probabilité que la femme soit enceinte en utilisant le théorème de Bayes. En effet, dans le cas d'un test positif,
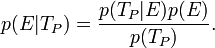
- C'est cette estimation a priori qui est systématiquement ignorée par les méthodes statistiques standard.
Notation d'évidence
Cette notation est souvent attribuée à I. J. Good. Ce dernier en attribuait cependant la paternité à Alan Turing et, indépendamment, à d'autres chercheurs dont Harold Jeffreys.
Dans la pratique, quand une probabilité est très proche de 0 ou de 1, il faut observer des éléments considérés eux-mêmes comme très improbables pour la voir se modifier. On définit l'évidence par :
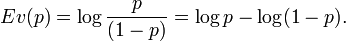
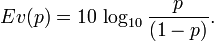
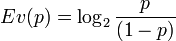
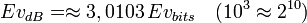
| Probabilité | Évidence (dB) | Évidence (bits) |
|---|---|---|
| 0,0001 | -40,0 | -13,3 |
| 0.0010 | -30,0 | -10,0 |
| 0,0100 | -20,0 | -6,6 |
| 0,1000 | -9,5 | -3,2 |
| 0,2000 | -6,0 | -2,0 |
| 0,3000 | -3,7 | -1,2 |
| 0,4000 | -1,8 | -0,6 |
| 0,5000 | 0,0 | 0,0 |
| 0,6000 | 1,8 | 0,6 |
| 0,7000 | 3,7 | 1,2 |
| 0,8000 | 6,0 | 2,0 |
| 0,9000 | 9,5 | 3,2 |
| 0,9900 | 20,0 | 6,6 |
| 0,9990 | 30,0 | 10,0 |
| 0,9999 | 40,0 | 13,3 |
Ev est une abréviation pour weight of evidence, parfois traduit en français par le mot évidence ; la formulation la plus conforme à l'expression anglaise d'origine serait le mot à mot poids de témoignage, mais par une coïncidence amusante « évidence » se montre très approprié en français pour cet usage précis.
C'est peu après les publications de Jeffreys qu'on découvrit qu'Alan Turing avait déjà travaillé sur cette question en nommant les quantités correspondantes log-odds dans ses travaux personnels.

















































