Lemme de Gauss (polynômes) - Définition
La liste des auteurs de cet article est disponible ici.
Généralisation
Une version de ce lemme est valide dans n'importe quel anneau factoriel A (c'est-à-dire possédant une bonne théorie de la divisibilité) à la place de l'anneau des entiers.
Voici l'équivalent du lemme de Gauss dans le cas général :
Théorème — Soient A un anneau factoriel et K son corps de fractions, un polynôme non constant f à coefficients dans A est irréductible si et seulement si il est primitif et irréductible dans l'ensemble des polynômes à coefficients dans K
.
Pour le démontrer, on définit d'abord le concept de polynôme primitif de A[X] comme un polynôme dont tous les coefficients sont premiers entre eux. On considère alors K le corps des fractions de A, et on montre que tout polynôme f s'écrit comme le produit d'une constante et d'un polynôme à coefficients dans A primitif. Cette constante est appelée contenu du polynôme et est défini à un facteur de A inversible dans A près. On démontre alors le théorème suivant :
Théorème — Soient A un anneau factoriel et K son corps de fractions. Soient f et g deux polynômes à une variable à coefficients dans K>. Alors :
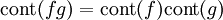
Un corollaire de ce lemme de Gauss est que pour tout anneau factoriel A, l'anneau des polynômes en plusieurs indéterminées A[X1,X2,...,Xn] est aussi factoriel. Le lemme de Gauss peut aussi être utilisé pour démontrer le critère d'irréductibilité d'Eisenstein.

















































