Logique (mathématiques élémentaires) - Définition

Approche d'une formalisation

Les bases

Soit P une proposition.
On dit que P est vraie ou fausse.

Soit P une propriété à un état. Alors non P est à l'état opposé.

On peut ainsi établir une table de vérité :

Et ceci montre que P = non non P.

Maintenant, et c'est ce qu'il y a de plus intéressant, concentrons-nous sur les relations :

Prenons les deux relations basiques : « et » et « ou » (il faut que P soit vrai et que Q soit vrai, ou respectivement, que P soit vrai ou Q soit vrai, pour que la relation soit vraie). On dit que R=P.Q=(P et Q) est vraie si tous deux sont vrais à la fois. On dit que R=P+Q=(P ou Q) est vraie si l'un ou l'autre est vrai.

On établit alors la table de vérité :

Soit P et Q deux propositions. Soit R la relation ⇒ (il suffit que)

Ceci est la définition de la relation implication.

De même, pour la relation (il faut que)

Enfin, pour que R: ⇔ soit vrai (équivalence), il faut que ⇒ et ⇐ soient vraies :

L'analyse de telles tables nous permet de montrer que, par exemple, dans une démonstration, pour que P ⇔ Q, il faut et il suffit que P ⇒ Q ET non P ⇒ non Q.

En effet :

On vient là de démontrer que la réciproque d'un théorème pouvait se montrer en partant de l'inverse des hypothèses pour arriver à l'inverse de la conclusion.

De la même façon, il est aisé de montrer avec ces tables de vérité que P ⇒ Q est équivalent à nonP ou Q. On laissera le lecteur faire le tableau afin de s'en convaincre.

La logique est donc à la base des mathématiques, et leur permet de faire toutes les démonstrations nécessaires pour les théorèmes les plus simples comme les plus complexes.

Résultats importants

Les lignes suivantes sont « vraies ». Il s'agit de relations vraies quelles que soient P et Q deux propositions.

• 
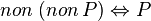
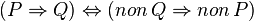
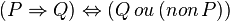
• , le deuxième membre de l'équivalence est souvent appelé la contraposée du premier membre.
• 
• , ce résultat est important lorsqu'on utilise un raisonnement par l'absurde: si on veut prouver une implication, on montre que sa négation conduit à une absurdité.