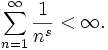Loi de Zipf - Définition

Point de vue théorique

Mathématiquement, il est impossible pour la version classique de la loi de Zipf de tenir exactement s'il existe une infinité de mots dans une langue, puisque pour toute constante de proportionnalité c > 0, la somme de toutes les fréquences relatives est proportionnelle à la série harmonique et doit être

Des observations citées par Léon Brillouin dans son livre Science et théorie de l'information suggérèrent qu'en anglais, les fréquences parmi les 1 000 mots les plus fréquemment utilisés étaient approximativement proportionnels à avec s juste légèrement plus grand que 1.

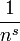
Tant que l'exposant s excède 1, il est possible pour une telle loi d'être vraie avec une infinité de mots, puisque si s > 1 alors

La valeur de cette somme est , où ζ est la fonction zêta de Riemann.

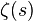
On sait toutefois que le nombre de mots d'une langue est limité. Le vocabulaire d'un enfant de 10 ans tourne autour de 5 000 mots, celui d'un adulte cultivé de 70 000^{[réf. souhaitée]}, et les dictionnaires en plusieurs volumes peuvent monter de 130 000 à 200 000.

Une loi à utiliser avec prudence

Il est tentant chaque fois que l'on voit des informations classées par ordre décroissant de se dire : « Elles doivent suivre une loi de Zipf ». Sans que ce soit nécessairement faux, il serait dangereux de le considérer comme allant de soi. Si nous prenons par exemple 100 entiers aléatoires entre 1 et 10 selon une loi uniforme, que nous les regroupons et que nous trions le nombre d'occurrences de chacun, nous obtenons la courbe ci-contre.

On admettra que si l'on se fie juste à une première impression visuelle, cette courbe paraît très « zipfienne », alors que c'est un tout autre modèle qui a engendré la série des données. Or il n'est pas possible de faire commodément un Chi2 sur la loi de Zipf, le tri des valeurs venant faire obstacle à l'usage d'un modèle probabiliste classique (n'oublions pas en effet que la répartition des occurrences n'est pas celle des probabilités d'occurrences, et que cela peut conduire à beaucoup d'inversions dans les tris).

La famille de distributions de Mandelbrot est certes démontrée adéquate de façon formelle pour un langage humain sous ses hypothèses de départ concernant le coût de stockage et le coût d'utilisation, qui découlent elles-mêmes de la théorie de l'information. En revanche il n'est pas prouvé qu'utiliser la loi de Zipf comme modèle pour la distribution des populations des agglomérations d'un pays soit un modèle pertinent — bien que le contraire ne soit pas prouvé non plus.

De plus l'estimation des paramètres de Mandelbrot à partir d'une série de données pose également problème et fait encore aujourd'hui l'objet de débats. Il ne saurait être question par exemple d'utiliser une méthode de moindres carrés sur une courbe en log-log dont de surcroît le poids des points respectifs est loin d'être comparable. Mandelbrot lui-même n'a apparemment pas fait de nouvelle communication sur le sujet depuis la fin des années 60.

Similarité

Le rapport entre lois de Zipf et de Mandelbrot d'une part, entre lois de Mariotte et de van der Waals d'autre part est similaire : on a dans les premiers cas une loi de type hyperbolique, dans les secondes une légère correction rendant compte de l'écart entre ce qui était prévu et ce qui est observé, et proposant une justification. Dans les deux cas, un élément de correction est l'introduction d'une constante manifestant quelque chose d'« incompressible » (chez Mandelbrot, le terme "a" de la loi). On peut aussi noter une ressemblance avec la loi de Benford qui porte sur le premier chiffre de chaque nombre d'un ensemble de données statistiques.