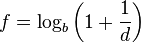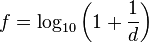Loi de Benford - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La loi de Benford, également appelée loi des nombres anormaux, n'est pas à proprement parler une loi, mais plutôt une observation empirique non démontrée ni expliquée mais qui se rencontre dans certains cas de figure et sur des ensembles de données bien particuliers. Dans une liste de données statistiques, elle énonce que le 1er chiffre non nul le plus fréquent est 1, pour près du tiers des observations. Puis le 2 est lui-même est plus fréquent que 3… et la probabilité d'avoir un 9 comme premier chiffre significatif n'est que de 4,6 %.
De façon générale, la loi donne la valeur théorique f de la fréquence d'apparition du premier chiffre d'un nombre d d'un résultat de mesure exprimé dans une base b donnée au moyen d'une unité.
Historique
Cette distribution a été observée une première fois en 1881 par l'astronome américain Simon Newcomb, dans un article de l'American Journal of Mathematics, après qu'il se fut aperçu de l'usure (et donc de l'utilisation) préférentielle des premières pages des tables de logarithmes (alors compilées dans des ouvrages). Cet article de Newcomb passe complètement inaperçu pendant cinquante-sept ans. Frank Benford, aux alentours de 1938, remarqua à son tour cette usure inégale, crut être le premier à formuler cette loi qui porte indûment son nom aujourd'hui, et arriva aux même résultats après avoir répertorié des dizaines de milliers de données (longueurs de fleuves, cours de la bourse, etc).
Système décimal
En particulier, pour le système décimal (base 10), on a donc :
Ce qui aboutit au tableau de résultats suivants :
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f | 30,1 | 17,6 | 12,5 | 9,7 | 7,9 | 6,7 | 5,8 | 5,1 | 4,6 |
| d | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| f | 30,1 | 47,7 | 60,2 | 69,9 | 77,8 | 84,5 | 90,3 | 95,4 | 100 |
Il existe également une discrète sur-représentation des premiers chiffres en ce qui concerne le second chiffre significatif du nombre. Cette sur-représentation tend à s'annuler au-delà.
Les exemples illustrant cette loi sont nombreux : prenez la suite des 100 premiers carrés ; la fréquence des nombres commençant par 1 est nettement supérieure à la fréquence des carrés commençant par 2, 3, 4, etc. En constituant la liste de 100 nombres, produits de deux ou trois nombres tirés au hasard (dans un grand intervalle), de nouveau la fréquence des nombres commençant par 1 est nettement plus élevée que les autres fréquences.
Les suites numériques qui se comportent exactement comme le stipule la loi de Benford sont, en fait, assez rares. Parmi celles-ci, on peut citer la suite de Fibonacci. Dans la vie réelle, la décroissance des probabilités suivant le premier chiffre est largement constatée, mais la convergence vers les valeurs de la loi de Benford n'est qu'approximative.
Au contraire, cette loi n'est pas vérifiée si la série de données comporte des contraintes quant à l'échelle des valeurs vraisemblables : par exemple, la taille des individus, lorsqu'elle est exprimée dans le système métrique, ne suit, à l'évidence, pas la loi de Benford puisque la quasi totalité des mesures commence par le chiffre « 1 ».