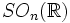Matrice orthogonale - Définition

Introduction

Une matrice carrée A (n lignes, n colonnes) à coefficients réels est dite orthogonale si elle vérifie :

, où A^t est la transposée de A et I_n est la matrice identité.

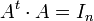
Propriétés des matrices orthogonales

• Une matrice A est orthogonale si et seulement si : A est inversible et son inverse est égale à sa transposée : A ^{− 1} = A^t.

• Une matrice est orthogonale si et seulement si tous ses vecteurs colonne sont orthogonaux entre eux et de norme 1. Ainsi une matrice orthogonale représente une base orthonormale.

• Également, une matrice est orthogonale si et seulement si sa transposée l'est, donc si et seulement si ses vecteurs ligne sont orthogonaux deux à deux et de norme 1.

• Le carré du déterminant d'une matrice orthogonale est égal à 1. Le déterminant d'une matrice orthogonale est donc égal à +1 ou -1. Si A est une matrice orthogonale et que son déterminant est +1 (respectivement -1), on dit que A est directe (respectivement indirecte).

• Le conditionnement d'une matrice orthogonale est égal à 1.

• La multiplication d'un vecteur par une matrice orthogonale préserve la norme de ce vecteur.

• L'ensemble de ces matrices est un groupe appelé groupe orthogonal et noté . Il s'interprète de manière géométrique comme étant l'ensemble des isométries vectorielles, aussi appelées automorphismes orthogonaux, de l'espace euclidien . Plus précisément, un endomorphisme d'un espace euclidien est orthogonal si, et seulement s'il existe une base orthonormée dans laquelle sa matrice est orthogonale (et si tel est le cas, sa matrice dans toute base orthonormée sera encore orthogonale).

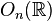
• L'ensemble des matrices orthogonales directes forme un sous-groupe du groupe orthogonal, appelé groupe spécial orthogonal et noté . Il s'interprète de manière géométrique comme étant l'ensemble des rotations de l'espace euclidien .