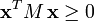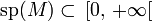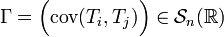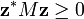Matrice positive - Définition

Introduction

En algèbre linéaire, la notion de matrice positive est analogue à celle de nombre réel positif ou nul.

Une matrice définie positive est une matrice positive inversible.

Matrice symétrique réelle positive

Soit M une matrice symétrique réelle d'ordre n. Elle est dite positive si elle vérifie l'une des deux propriétés équivalentes suivantes :

1.	La forme bilinéaire symétrique qu'elle représente est positive, c'est-à-dire : pour toute matrice colonne à n éléments réels, on a .
2.	Les valeurs propres de M (qui sont automatiquement réelles) sont positives ou nulles, c'est-à-dire : .

Exemples

• Soit f une fonction réelle de n variables réelles définie et de classe C² sur un ouvert de . En tout point où f atteint un minimum local, sa matrice hessienne est positive (condition nécessaire d'ordre 2 pour un point de minimum local).
• Étant donné un vecteur aléatoire à valeurs dans dont chaque composante admet une variance, on définit sa matrice des covariances :

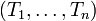
Celle-ci est positive. En effet, pour toute matrice colonne à n éléments réels notés  :

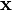
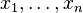
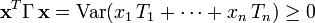
Elle est définie positive si et seulement si la seule combinaison linéaire de qui soit certaine est celle dont tous les coefficients sont nuls.

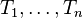
Propriétés

• Pour toute matrice réelle A, la matrice A^T.A est une matrice symétrique positive. De plus si A est une matrice carrée inversible, A^T.A est définie positive.
• Toute matrice réelle symétrique positive admet une unique racine carrée réelle symétrique positive. Plus formellement :

.

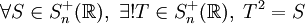
Ce résultat se généralise aux racines n-ièmes.

Matrice hermitienne positive

On étend les propriétés et définitions précédentes aux matrices complexes hermitiennes.

Soit M une matrice hermitienne d'ordre n. Elle est dite positive si elle vérifie l'une des deux propriétés équivalentes suivantes :

1.	Pour toute matrice colonne à n éléments complexes, on a (où désigne la matrice transconjuguée de ).
2.	Toutes les valeurs propres de M sont positives ou nulles, c'est-à-dire : .