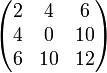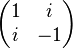Matrice symétrique - Définition

Introduction

En algèbre linéaire et bilinéaire, une matrice symétrique est une matrice carrée qui est égale à sa propre transposée.

Exemples

Intuitivement, les coefficients d'une matrice symétrique sont symétriques par rapport à la diagonale principale (du coin en haut à gauche jusqu'à celui en bas à droite). La matrice suivante est donc symétrique :

Toute matrice diagonale est symétrique.

Matrices symétriques réelles

• Dans un espace euclidien, une matrice représentant un endomorphisme dans une base orthonormée est symétrique si et seulement si l'endomorphisme est autoadjoint.
• Le théorème spectral en dimension finie énonce que toute matrice symétrique à coefficients réels est diagonalisable à l'aide d'une matrice orthogonale. Ses valeurs propres sont donc réelles, et ses sous-espaces propres sont orthogonaux. Une démonstration est proposée dans l'article Endomorphisme autoadjoint.
• Remarque : une matrice symétrique à coefficients complexes peut ne pas être diagonalisable. Exemple :

En effet, cette matrice admet 0 comme seule valeur propre ; si elle était diagonalisable, elle serait nulle.

L'analogue complexe des matrices symétriques réelles est en fait les matrices autoadjointes (qui, elles, sont diagonalisables).

Matrices symétriques positives

• Une matrice symétrique réelle S est dite positive si la forme bilinéaire symétrique qu'elle représente est positive, c'est-à-dire si pour toute matrice colonne réelle X,

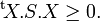
• Elle est dite définie positive si sa forme bilinéaire est de plus définie, c'est-à-dire si pour toute matrice colonne réelle X,

Propriétés

• Une matrice représentant une forme bilinéaire est symétrique si et seulement si cette dernière est symétrique.
• L'ensemble des matrices symétriques d'ordre n à coefficients dans un corps est un sous-espace vectoriel de dimension n(n+1)/2 de l'espace vectoriel des matrices carrées d'ordre n, et si la caractéristique du corps est différente de 2, un sous-espace supplémentaire est celui des matrices antisymétriques.

Utilisations concrètes

• Une matrice symétrique d'ordre 3 représente une conique en coordonnées homogènes dans un plan projectif construit à partir de .