Méthode de Monte-Carlo cinétique - Définition

Introduction

La méthode de Monte-Carlo cinétique, kinetic Monte Carlo (KMC) en anglais, est une méthode de Monte-Carlo de simulation informatique permettant de simuler des processus se produisant à des taux connus. En cela elle permet de simuler exactement le comportement de systèmes évoluant selon une équation maîtresse.

C’est une méthode peu gourmande en temps de calcul permettant d’explorer des échelles de temps et d’espace importantes. Elle permet en particulier d’étudier des phénomènes à probabilité faible.

Les taux doivent être connus à l'avance, l'algorithme ne fait que les utiliser.

L'algorithme Monte-Carlo cinétique porte plusieurs noms : algorithme à temps de résidence residence-time algorithm, Bortz-Kalos-Liebowitz (BKL) (Bortz 1975), n-fold way algorithme, algorithme ou méthode de Monte-Carlo dynamique ou encore algorithme de Gillespie (Gillespie 1976), ...

Algorithme

Taux de transfert indépendants du temps

À chaque étape, le système dispose de plusieurs états accessibles, les taux de transferts vers chacun des états étant supposés connus.

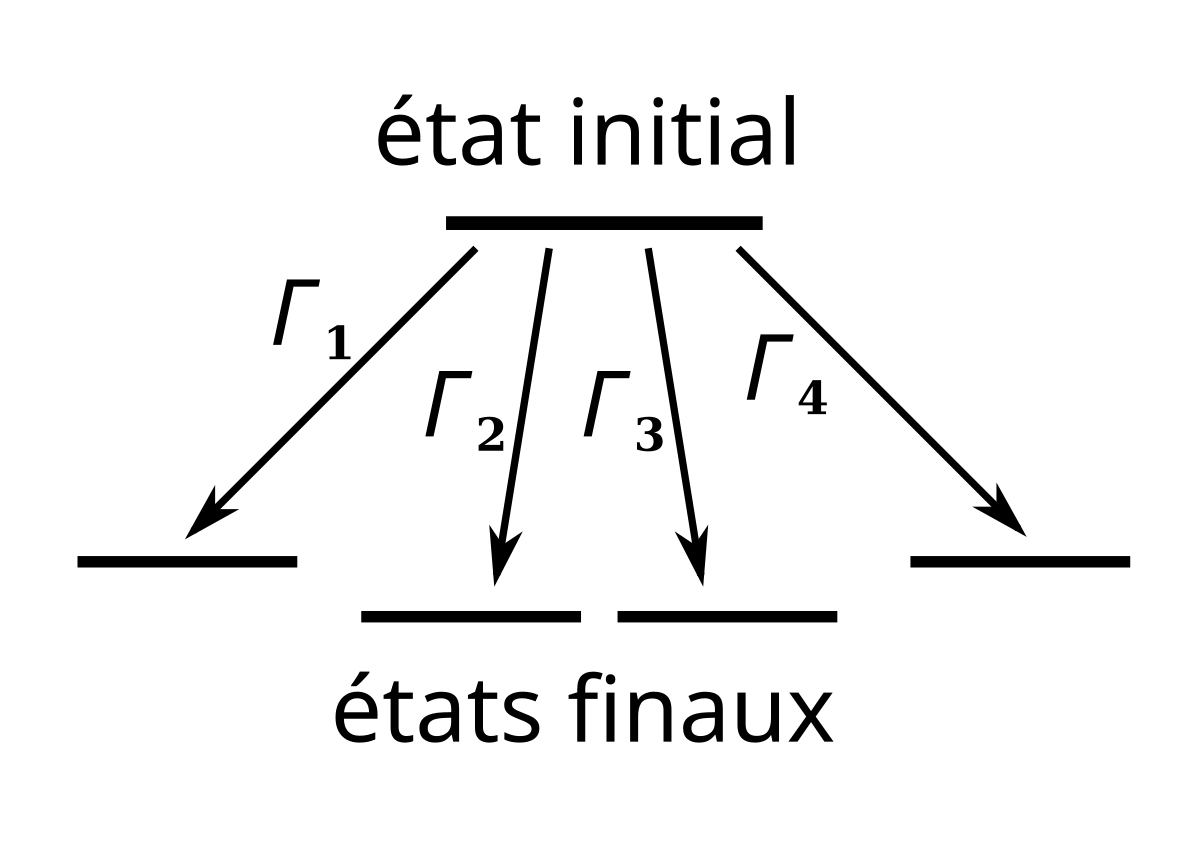
L'algorithme de Monte-Carlo cinétique est utilisé pour modéliser les sauts aléatoires d'un système d'un état initial vers un ensemble d'états finaux possibles, le nombre total N_t de sauts effectués à un instant t étant modélisé par un processus de Poisson. À l'issue de chaque saut, on évalue les conséquences de la transition entre l'état initial et le nouvel état : arrêt de la simulation, nouvelle étape de simulation avec ou sans changement des taux de transfert, etc.

Choix de l'état final : une variable aléatoire est tirée entre 0 et Γ_tot ; la probabilité que le système évolue vers l'état i est proportionnelle à Γ_i.

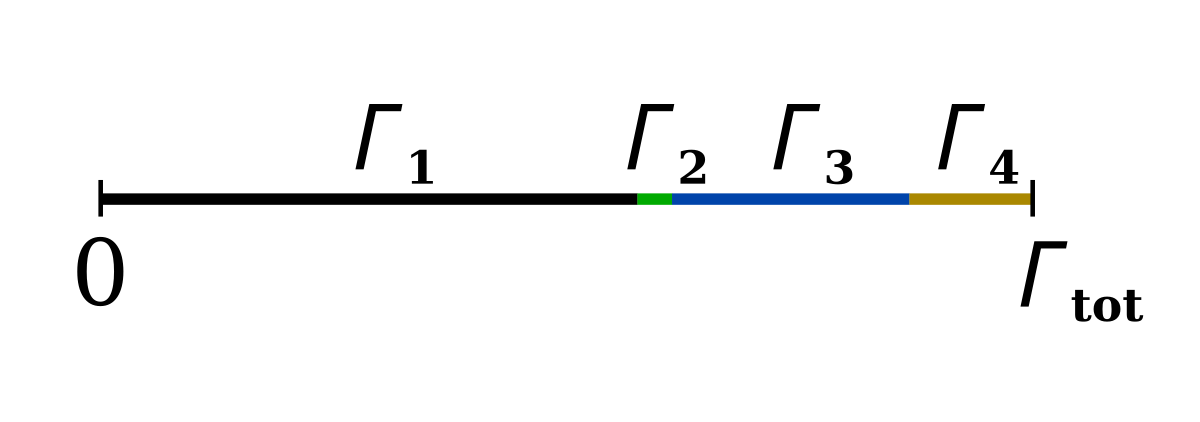
Pour se familiariser avec l'algorithme, on suppose dans cette section que les taux de transfert restent constants pendant l'intervalle de temps séparant deux sauts successifs, ce qui correspond à un processus de Poisson homogène. L'algorithme est donné par les étapes suivantes :

1. On note t₀ le temps actuel.
2. On forme une liste de l'ensemble des taux de transfert Γ_i du système, i = 1,..., N, et l'on note Γ_tot = ∑ Γ_i le taux de transfert total.
3. Le temps T au bout duquel le système quitte son état initial est donné par la formule T = – ln(U)/Γ_tot, où U est une variable aléatoire uniformément répartie entre 0 et 1.
4. On choisit un deuxième nombre aléatoire U' uniformément réparti entre 0 et Γ_tot qui va servir à tirer au hasard l'état final de la transition (voir la figure ci-contre).
5. Si U' est compris entre 0 et Γ₁, le système transite vers l'état 1 ; entre Γ₁ et Γ₁+Γ₂ le système transite vers l'état 2 ; et si U' est entre S_i-1 et S_i, où S₀ = 0 et , le système transite vers l'état i.
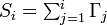
6. Prendre en compte cette transition en effectuant les calculs correspondants.
7. Changer le temps en t₀+T et recommencer l'étape 1.

Justification de l'étape 3 

La variable aléatoire T représente le temps d'attente avant que le système quitte l'état initial. Sa densité de probabilité est ρ_T(t) = Γ_totexp( − Γ_tott) pour t ∈ [0, +∞[. La formule utilisée dans l'étape 3 correspond au changement de variable U = exp( – Γ_totT), ce qui donne bien la même densité de probabilité : si l'on considère ρ_U(u) = 1 sur ]0, 1].

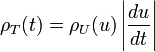
Justification de l'étape 5 

La probabilité que l'état final soit l'état i est p_i = ^Γ_i⁄_Γtot, ce qui est égal à

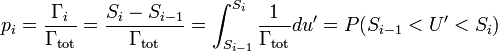
Cet algorithme simule l'évolution du système au cours du temps et n'a pas a priori de condition d'arrêt. En pratique, on arrête la boucle lorsque le temps dépasse une certaine valeur ou lorsque le système a effectué un certain nombre de sauts ; la suite des états i suivis par le système au cours du temps est appelée une trajectoire Monte-Carlo ; on répète ensuite cette boucle de manière à obtenir un nombre important de trajectoires, auxquelles on peut appliquer une analyse statistique. Puisque les trajectoires sont indépendantes les unes des autres, il est facile de paralléliser l'algorithme de Monte-Carlo cinétique.

Taux de transfert variants au cours du temps

L'algorithme est essentiellement le même si l'on suppose que les Γ_i dépendent du temps, mais les formules reliant U et U' à T et à l'état final i sont différentes :

• T est donné par la formule , qu'il est nécessaire d'inverser pour trouver T ;
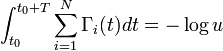
• Les sommes S_i sont à évaluer en t = t₀+T. Ceci provient du fait que jusqu'au temps t₀+T le système est encore dans l'état initial (Chotia 2008). Cette absence de "mémoire" est caractéristique d'un processus de Markov.