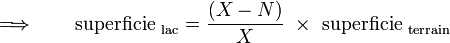Méthode de Monte-Carlo - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
Résolution du Problème du voyageur de commerce
La résolution du problème du voyageur de commerce est difficile, du fait de la complexité du problème, l'emploi de méthodes d'optimisation probabilistes peut s'avérer efficace pour obtenir une approximation de la meilleure solution, en un temps plus court que pour des méthodes déterministes.
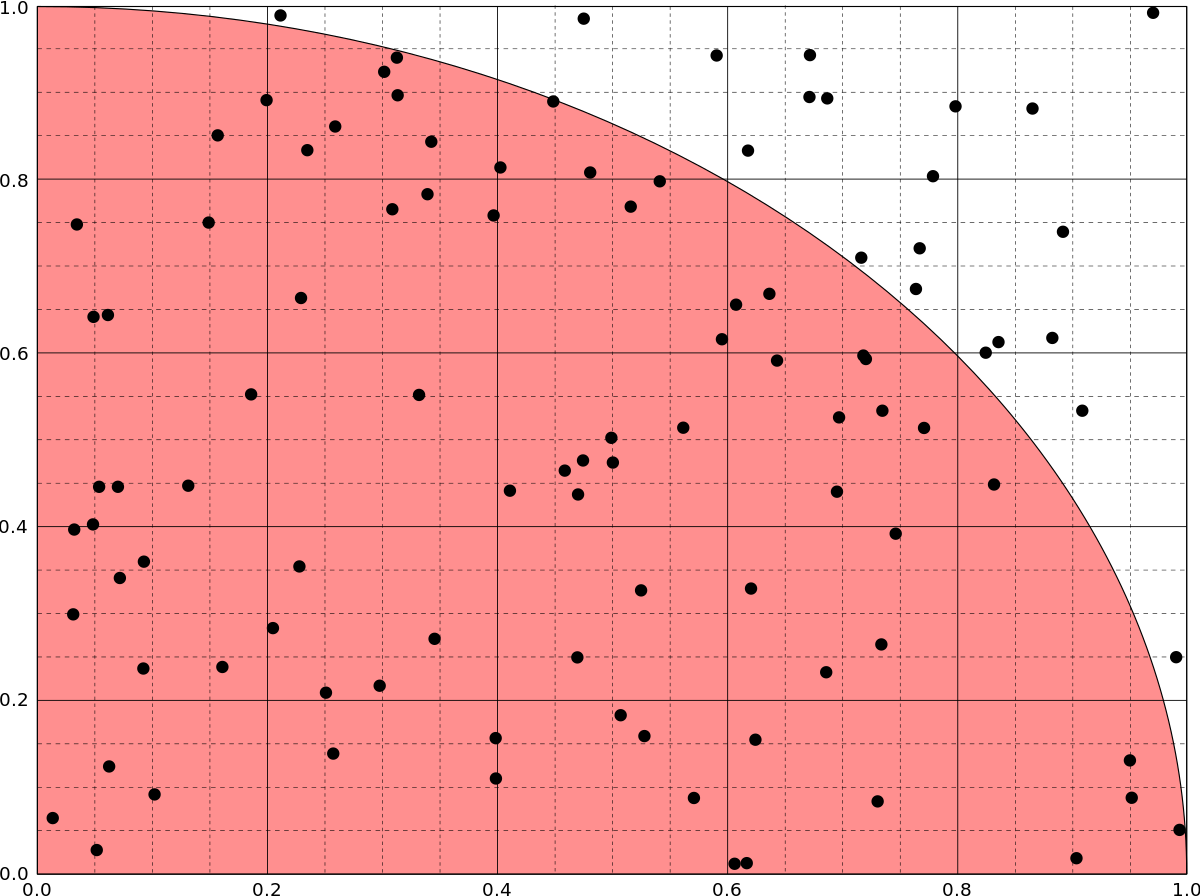
Détermination de la valeur de π (pi)
Cette méthode est proche de l'expérience de l'aiguille de Buffon.
Soit un point
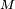
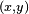
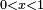
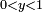
On tire aléatoirement les valeurs de


Si
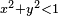
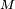
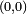
La probabilité que le point
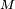
En faisant le rapport du nombre de points dans le disque par rapport au nombre de tirages on obtient une approximation du nombre π/4 si le nombre de tirages est grand.
Détermination de la superficie d'un lac
Cet exemple est un classique en vulgarisation de la méthode de Monte-Carlo. Soit une zone rectangulaire ou carrée dont les côtés sont de longueur connue. Au sein de cette aire se trouve un lac dont la superficie est inconnue. Grâce aux mesures des côtés de la zone, on connaît l'aire du rectangle. Pour trouver l'aire du lac, on demande à une armée de tirer X coups de canon de manière aléatoire sur cette zone. On compte ensuite le nombre N de boulets qui sont restés sur le terrain ; on peut ainsi déterminer le nombre de boulets qui sont tombés dans le lac : X-N. Il suffit ensuite d'établir un rapport entre les valeurs :
Par exemple, si le terrain fait 1000 m2, que l'armée tire 500 boulets et que 100 projectiles sont tombés dans le lac, alors une estimation de la superficie du plan d'eau est de : 100*1000/500 = 200 m2.
La qualité de l'estimation s'améliore en augmentant le nombre de tirs et en s'assurant que les artilleurs ne visent pas toujours le même endroit mais couvrent bien la zone. Cette dernière remarque est à mettre en parallèle avec la qualité du générateur aléatoire qui est primordiale pour avoir de bons résultats dans la méthode de Monte-Carlo. Un générateur biaisé est comme un canon qui tire toujours au même endroit : les informations qu'il apporte sont réduites.
Application au modèle d'Ising
Estimation de la valeur d'un coup au Go
Aux Échecs, il est facile de mesurer la valeur d'une position, et donc d'un coup y menant, en comptant le nombre de pièces sur l'échiquier, en les pondérant (1 point par pion, 5 par tour...), et en ajustant la valeur trouvée par les libertés, les protections des pièces... Cela n'est pas possible au go. On a alors recours à une analyse de Monte-Carlo : on joue "au hasard" un grand nombre de parties, et on comptabilise la proportion que l'on en gagne. Cette estimation statistique peut s'affiner en biaisant le hasard en évitant les coups stupides. Voir l'article dédié.
Estimation de la valeur d'un coup aux Échecs
Parfois, pour savoir si un coup hasardeux doit être fait (échange de pièces par exemple), lorsqu'on manque d'information, ou pour choisir entre plusieurs coups menant tous à des pertes de matériel, il est possible de lancer plusieurs parties rapides au hasard, pour savoir quelle est la moins pire ou la meilleure des solutions.
Estimation de la véracité de rumeurs
Pour savoir si une rumeur est probablement vraie, on teste la recherche sur internet, et son contraire. Il suffit de comparer les résultats sur un même moteur de recherche. C'est une méthode simple, rapide et gratuite, mais non fiable, par la multiplicité des sources non vérifiées. Exemples :
- "Ben laden est vivant" : environ 99 500 résultats sur Google, le 25 décembre 2010.
- "Ben laden est mort" : environ 292 000 résultats sur Google, le 25 décembre 2010, soit environ trois fois plus.
Il est donc plus probable, mais pas certain, qu'Ossama Ben Laden soit décédé. (Estimer la date de décès est plus difficile "Ben laden est mort le" donnant une date qui a pu être copiée de site en site).
De même, à titre de référence :
- "François mitterrand est mort" : environ 44 900 résultats sur Google, le 25 décembre 2010.
- "François mitterrand est vivant" : 5 résultats sur Google, le 25 décembre 2010.