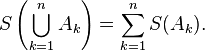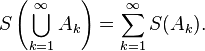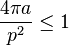Superficie - Définition

Introduction

L'aire ou la superficie est une mesure d'une surface. Par métonymie, on désigne souvent cette mesure par le terme « surface » lui-même (par exemple, on parle de la « surface d'un appartement » alors qu'il faudrait parler de sa superficie). Le terme « aire » (du bas latin aera : « espace plan ») est utilisé en mathématiques, alors que « superficie » lui est préféré dans les autres domaines.

En pratique, la superficie est utilisée pour déterminer les prix d'un appartement, le rendement d'un terrain agricole ou la quantité de peinture à utiliser pour colorer une surface. L'unité d'aire, dans le système international d'unités est le mètre carré (m²), bien que l'hectare (1 ha = 10 000 m²) lui soit souvent préféré pour les terrains.

La détermination de la surface de terrains agricoles puis de figures abstraites a été à l'origine de la géométrie et un moteur important du développement de cette science et des mathématiques en général.

Du point de vue mathématique, l'aire d'une surface est un nombre réel positif qui répond à des propriétés d'additivité (si une surface est partagée, la somme des aires de chaque morceau est égale à la surface initiale) et de conservation par des isométries (déplacer une surface ne modifie pas son aire). L'aire des surfaces complexes est déterminée à l'aide de ces propriétés et du fait que l'aire d'un carré de côté 1 est égale à 1 à l'aide d'un raisonnement par découpage, déplacement et collage éventuellement complété par un passage à la limite ou d'autres méthodes, comme le calcul intégral.

Propriétés

La superficie S d'une surface plane suit quatre propriétés :

1. La superficie d'une surface plane est un nombre positif ou nul.
2. Une unité de longueur étant choisie, la superficie du carré de côté 1 est égale à 1.
3. La superficie est additive. Cela signifie que, les superficies de deux surfaces disjointes A et B étant données, la superficie de leur union est la somme de leurs superficies :

   S(A ∪ B) = S(A) + S(B).

   Cette propriété peut être interprétée ainsi : si on « découpe » une figure, on obtient deux figures dont les aires additionnées redonnent l'aire de départ.

4. La superficie est invariante par isométrie. Cela signifie qu'une figure peut être déplacée ou retournée sans que cela modifie sa superficie.

La propriété d'additivité est étendue, par récurrence, à un entier naturel n supérieur à deux quelconque : si A₁, A₂, ... A_n sont des surfaces deux à deux disjointes d'aires respectives S(A₁), S(A₂), ... S(A_n), alors

S(A₁ ∪ A₂ ∪ ... ∪A_n) = S(A₁) + S(A₂) + ... + S(A_n)

ce qui se note plus rigoureusement :

Mais cette propriété d'additivité finie ne suffit pas, ne serait-ce que pour prouver la formule de calcul de l'aire d'un disque (voir plus bas). Elle est donc étendue à une famille infinie dénombrable de surfaces planes (A_n)_{n∈ N^∗} deux à deux disjointes dont les aires sont supposées connues, avec le résultat analogue au précédent :

On parle alors de σ-additivité (« sigma-additivité »).

Problèmes d'aire

Quadrature du cercle

Un problème d'aire a traversé les siècles, depuis au moins Anaxagore (V^e siècle av. J.-C.) jusqu'à 1882, lorsque Ferdinand von Lindemann prouve que π est un nombre transcendant : celui de la quadrature du cercle qui consiste à construire, à la règle et au compas, un carré d'aire égale à celle d'un disque donné.

Confusion entre aire et périmètre

Le périmètre est, avec l'aire, l'une des deux mesures principales des figures géométriques planes. Il est fréquent de confondre ces deux notions ou de croire que, plus l'une est grande, plus l'autre l'est aussi. En effet l'agrandissement (ou la réduction) d'une figure géométrique fait croître (ou décroître) simultanément son aire et son périmètre. Par exemple, si un terrain est représenté sur une carte à l'échelle 1:10 000, le périmètre réel du terrain peut être calculé en multipliant le périmètre de la représentation par 10 000 et l'aire en multipliant celle de la représentation par 10 000². Il n'existe cependant aucun lien direct entre l'aire et le périmètre d'une figure quelconque. Par exemple, un rectangle possédant une aire égale à un mètre carré peut avoir comme dimensions, en mètres : 0,5 et 2 (donc un périmètre égal à 5 m) mais aussi 0,001 et 1000 (donc un périmètre de plus de 2 000 m). Proclus (V^e siècle) rapporte que des paysans grecs se sont partagés « équitablement » des champs suivant leurs périmètres, mais avec des aires différentes. Or, la production d'un champ est proportionnelle à l'aire, non au périmètre : certains paysans naïfs ont pu obtenir des champs avec de longs périmètres, mais une aire (et donc une récolte) médiocre.

Isopérimétrie, surface minimale

L'isopérimétrie traite, en particulier, la question de trouver la surface la plus vaste possible, pour un périmètre donné. La réponse est intuitive, c'est le disque. Ceci explique pourquoi, notamment, les yeux à la surface d'un bouillon ont une forme circulaire.

Ce problème, d'apparence anodin, fait appel à des théories sophistiquées pour obtenir une démonstration rigoureuse. On simplifie parfois le problème isopérimétrique en limitant les surfaces autorisées. Par exemple on cherche le quadrilatère ou le triangle d'aire la plus vaste possible, toujours pour un périmètre donné. Les solutions respectives sont le carré et le triangle équilatéral. De manière générale, le polygone à n sommets ayant la plus grande surface, à périmètre donné, est celui qui se rapproche le plus du cercle, c'est le polygone régulier.

L'isopérimétrie ne se limite pas à ces questions. On recherche aussi une zone d'aire la plus vaste possible pour un périmètre donné, avec des géométries différentes. Par exemple, dans le cas d'un demi-plan, la réponse est le demi-disque.

Ce concept donne naissance à une famille de théorèmes, dit isopérimétriques, à des majorations dites inégalités isopérimétriques, ainsi qu'à un rapport, appelé quotient isopérimétrique. L'inégalité isopérimétrique indique qu'une surface de périmètre p et d'aire a vérifie la majoration suivante :

Le terme de gauche, est appelé quotient isopérimétrique, il est égal à 1 si, et seulement si la surface est un disque.

Si l'origine de cette question date d'au moins 2 900 ans, ce n'est qu'en 1895, à l'aide de méthodes dérivées du théorème de Minkowski que la question est définitivement résolue sous sa forme antique. Ces méthodes permettent de démontrer le théorème isopérimétrique et de le généraliser à des dimensions supérieures dans le cas d'une géométrie euclidienne.

Le problème d'isopérimétrie dans l'espace à trois dimensions consiste à chercher, le plus grand volume contenu dans une surface d'aire donnée. La réponse est la sphère, ce qui entraîne notamment la forme des bulles de savon.

Voir l'article isopérimétrie pour les aspects élémentaires de cette question. Des éléments de réponse, faisant usage d'outils mathématiques plus sophistiqués, sont proposés dans l'article Théorème isopérimétrique.

Une surface minimale est une surface de l'espace à trois dimensions qui, sous certaines contraintes, minimise l'aire au voisinage de chacun de ses points. Cela signifie qu'une petite variation de cette surface rend l'aire plus grande. Pour un ensemble donné de contraintes, il peut exister plusieurs surfaces minimales. Les surfaces minimales sont spontanément prises par un film de savon qui s'appuie sur un cadre car de telles surfaces minimisent également les forces exercées sur le film. La recherche de telles surfaces est appelée en mathématiques problème de Plateau, elle nécessite des raisonnements de calcul différentiel.

Grande surface

A contrario, le problème d'obtenir, pour un volume donné, la figure avec la plus grande superficie possible se pose. Une solution mathématiquement simple existe : une surface sans épaisseur possède un volume nul. De telles formes se trouvent dans la nature : une feuille de plante verte est généralement très peu épaisse mais large, afin d'exposer la plus grande surface possible au soleil, pour favoriser la photosynthèse. Mais une grande surface du limbe foliaire de la feuille favorise également la transpiration, les plantes devant lutter contre des périodes de sécheresse (pins, cactus...) ont ainsi souvent des feuilles plus épaisses afin de diminuer leur superficie et donc lutter contre le dessèchement.

Une autre stratégie possible consiste à prendre une solide et à le percer d'un grand nombre de trous. Par exemple, l'éponge de Menger est construite à partir d'un cube qu'on partage trois tranches égales suivant chacune des trois dimensions. Cela donne vingt-sept cubes égaux, puis on enlève les cubes centraux. On obtient alors un nouveau solide, de volume inférieur et d'aire supérieure au précédent, constitué de vingt cubes. Puis on reprend le même procédé pour chacun de ces vingt cubes, puis à nouveau pour les cubes ainsi obtenus, etc. En répétant le procédé indéfiniment, on obtient un objet fractal qui possède une aire infinie et un volume égal à zéro, tout en ayant des dimensions (longueur, largeur, profondeur) égales à celles du cube de départ. Des formes très découpées comme l'éponge de Menger se trouvent dans la nature, lorsqu'il s'agit de favoriser les échanges entre deux milieux : par exemple les poumons de mammifères (afin de maximiser les échanges gazeux dans un volume réduit), les branchies, intestins...

La surface spécifique d'un matériau est sa superficie par unité de masse : plus la surface spécifique est grande, plus l'objet peut échanger avec son environnement, plus il est poreux. La surface spécifique est notamment une caractéristique physique importante d'un sol, qui détermine sa capacité à retenir des éléments nutritifs et à les échanger avec des plantes.