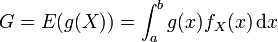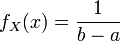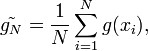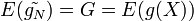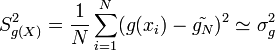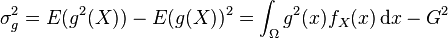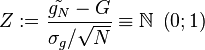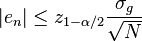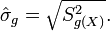Méthode de Monte-Carlo - Définition

Introduction

Le terme méthode de Monte-Carlo, ou méthode Monte-Carlo, désigne toute méthode visant à calculer une valeur numérique en utilisant des procédés aléatoires, c'est-à-dire des techniques probabilistes. Le nom de ces méthodes, qui fait allusion aux jeux de hasard pratiqués à Monte-Carlo, a été inventé en 1947 par Nicholas Metropolis (en), et publié pour la première fois en 1949 dans un article co-écrit avec Stanislas Ulam.

Les méthodes de Monte-Carlo sont particulièrement utilisées pour calculer des intégrales en dimensions plus grandes que 1 (en particulier, pour calculer des surfaces et des volumes). Elles sont également couramment utilisées en physique des particules, où des simulations probabilistes permettent d'estimer la forme d'un signal ou la sensibilité d'un détecteur. La comparaison des données mesurées à ces simulations peut permettre de mettre en évidence des caractéristiques inattendues, par exemple de nouvelles particules.

La méthode de simulation de Monte-Carlo permet aussi d'introduire une approche statistique du risque dans une décision financière. Elle consiste à isoler un certain nombre de variables-clés du projet, tels que le chiffre d'affaires ou la marge, et à leur affecter une distribution de probabilités. Pour chacun de ces facteurs, un grand nombre de tirages aléatoires est effectué dans les distributions de probabilité déterminées précédemment, afin de trouver la probabilité d'occurrence de chacun des résultats.

Le véritable développement des méthodes de Monte-Carlo s'est effectué sous l'impulsion de John von Neumann et Stanislas Ulam notamment, lors de la Seconde Guerre mondiale et des recherches sur la fabrication de la bombe atomique. Notamment, ils ont utilisé ces méthodes probabilistes pour résoudre des équations aux dérivées partielles dans le cadre de la Monte-Carlo N-Particle transport (MCNP).

Théorie

Nous disposons de l'expression de l'espérance mathématique d'une fonction g de variable aléatoire X, résultant du théorème de transfert, selon lequel

où f_X est une fonction de densité sur le support [a;b]. Il est fréquent de prendre une distribution uniforme sur [a;b]:

Ceci peut être étendu aux probabilités discrètes en sommant grâce à une mesure ν discrète, de type Dirac.

L'idée est de produire un échantillon (x₁,x₂,...,x_N) de la loi X (donc d'après la densité f_X) sur le support [a;b], et de calculer un nouvel estimateur dit de Monte-Carlo, à partir de cet échantillon.

La loi des grands nombres suggère de construire cet estimateur à partir de la moyenne empirique :

qui se trouve être, par ailleurs, un estimateur sans biais de l'espérance.

Ceci est l'estimateur de Monte-Carlo. Nous voyons bien qu'en remplaçant l'échantillon par un ensemble de valeurs prises dans le support d'une intégrale, et de la fonction à intégrer, nous pouvons donc construire une approximation de sa valeur, construite statistiquement.

Cette estimation est sans-biais, dans le sens où

Il faut aussi quantifier la précision de cette estimation, via la variance de

.

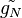
Si l'échantillon est supposé iid, cette variance est estimée à l'aide de la variance empirique

avec

Par le théorème de la limite centrale, on sait que la variable :

qui est centrée et réduite, suit approximativement la loi normale centrée réduite, ou loi de Gauss. Il est alors possible de construire des intervalles de confiance, ce qui permet d'encadrer l'erreur commise en remplaçant G par . Si cette erreur est dénotée e_n, alors pour un niveau de risque α donné, on a:

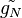
avec probabilité 1 − α. Le réel z_{1 − α / 2} est le quantile de la loi normale centrée réduite. Par exemple, au niveau de risque , on trouve dans les tables z_{1 − α / 2} = 1,96 et l'erreur est majorée par . Cette méthode permet donc de quantifier l'erreur commise, à condition d'estimer σ_g par sa contre-partie empirique

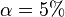
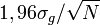
On voit ainsi que l'erreur est de l'ordre de N ^{− 1 / 2}: par exemple, multiplier la taille de l'échantillon par 100 permet de diviser par 10 l'erreur d'estimation.

Il est à noter qu'en pratique, σ_g n'est pas connu et doit être estimé ; comme précisé plus-haut, on peut utiliser sa contre-partie empirique. Diverses méthodes, dites techniques de réduction de la variance, permettent d'améliorer la précision — ou de diminuer le temps de calcul — en remplaçant g(X) par une autre variable aléatoire. Ces techniques rentrent en général dans l'une des classes suivantes : l'échantillonnage préférentiel, les variable de contrôle, la variable antithétique, la stratification (Monte-Carlo) et le conditionnement (Monte-Carlo).