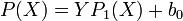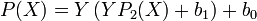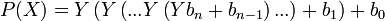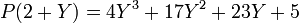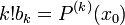Méthode de Ruffini-Horner - Définition
La liste des auteurs de cet article est disponible ici.
Valeur approchée d'une racine
Pour chercher la valeur approchée x d'une racine d'un polynôme P, on cherche un entier
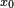
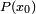
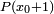
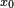
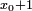
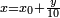
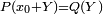
Il s'agit alors de chercher une racine de R comprise entre 0 et 10 en utilisant un processus analogue : on cherche un entier
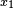
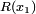
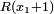
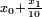
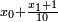
On détermine ainsi les décimales successives du développement décimal de x.
Exemple : Algorithme de Ruffini-Horner pour l'extraction de la racine cubique de 18.
Il s'agit de trouver un réel x racine du polynôme
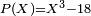
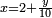
| Coefficients de P | 1 | 0 | 0 | - 18 |
| Coeficients de P1 | 1 | 2 | 4 | - 10 |
| Coeficients de P2 | 1 | 4 | 12 | |
| Coeficients de P3 | 1 | 6 | ||
| Coeficients de P4 | 1 |
Le réel x est racine cubique de 18 si
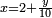
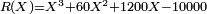
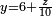
| Coefficients de R | 1 | 60 | 1200 | -10000 |
| Coeficients de R1 | 1 | 66 | 1596 | -424 |
| Coeficients de R2 | 1 | 72 | 2028 | |
| Coeficients de R3 | 1 | 78 | ||
| Coeficients de R4 | 1 |
Le réel y est racine de R si
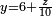
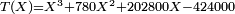
Changement de variable
L'algorithme précédent permet donc d'effectuer la division euclidienne du polynome P par
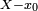
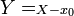
En utilisant de nouveau l'algorithme pour
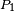
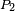
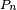
...
Les nombres
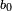
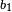
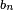
Illustration pratique : Si
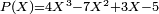
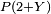
| Coefficients de P | 4 | − 7 | 3 | − 5 |
| Coeficients de P1 | 4 | 8 − 7 = 1 | 2 + 3 = 5 | 10 − 5 = 5 |
| Coeficients de P2 | 4 | 8 + 1 =9 | 18 + 5 = 23 | |
| Coeficients de P3 | 4 | 8 + 9 =17 | ||
| Coeficients de P4 | 4 |
Donc
Dérivées successives de P en x0
Cette propriété apparaît ici en dernière position alors qu'elle est la propriété initiale mise en évidence par Ruffini et Horner. Cependant, comme une démarche purement algébrique est possible, celle-ci, plus simple, a été présentée d'abord. Le même algorithme permet de déterminer aussi la valeur de
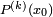
Si on note Q(Y) = P(a + Y), les coefficients bk de Q, trouvés par la méthode de Ruffini-Horner vérifient l'égalité