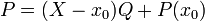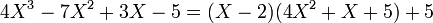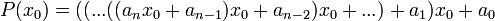Méthode de Ruffini-Horner - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Connue sous le nom de méthode de Horner, règle de Ruffini ou algorithme de Ruffini-Horner, cette méthode se décline sur plusieurs niveaux. Elle permet de calculer la valeur d'un polynôme en
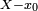
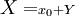
Histoire
La méthode de Ruffini-Horner de recherche d'une valeur approchée de racine d'un polynôme est publiée à quelques années d'intervalle par Paolo Ruffini (1804-1807-1813) et par William George Horner (1819-1845 posthume) mais il semble bien que Horner n'ait pas eu connaissance des travaux de Ruffini. La méthode de Horner est ensuite popularisée par les mathématiciens De Morgan et J.R. Young. Dans leurs premières publications, ces deux auteurs utilisent des méthodes de dérivations pour effectuer le changement de variable X = x0 + Y. Par la suite, ils présentent des versions ne faisant appel qu'à des techniques algébriques. La méthode de Ruffini-Horner est difficilement exploitable si le polynôme possède deux racines trop proches. Ruffini n'évoque pas ce problème mais Horner propose une procédure spéciale pour ce cas-là.
En tant que technique de changement de variable, on retrouve des algorithmes analogues, en Chine, pour l'extraction de racine n-ième, dans les Neuf Chapitres (263 après J.C)et dans l'œuvre de Al Samaw'al (XIIe siècle). Mais il semble bien que Sharaf al-Dīn al-Tūsī (XIIe siècle) soit le premier à l'utiliser dans le cas général d'une équation de degré 3.
Quotient d'un polynôme par X - x0
Cette même méthode permet aussi d'obtenir la division d'un polynôme par
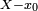
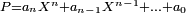
La division euclidienne de P par
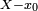
où Q est un polynôme de degré n - 1.
Si on écrit
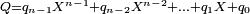
-
-
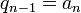
-
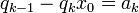
-
Soit encore
-
-
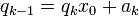
-
Les n valeurs de la suite q calculées ici sont précisément les n valeurs successives calculées dans le paragraphe précédent pour évaluer
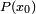
Application pratique : Division euclidienne de
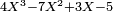
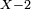
Il suffit de reprendre le tableau précédemment construit et de lire dans les cases de la seconde ligne les coefficients de Q.
| Coefficients de P | 4 | − 7 | 3 | − 5 |
| Coeficients de Q | 4 | 8 − 7 = 1 | 2 + 3 = 5 | Reste = 10 − 5 = 5 |
Donc
Valeur d'un polynôme en un point
Soit
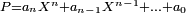
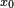
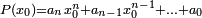
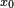
Si on calcule
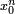
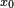
On peut améliorer la vitesse du calcul de
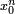
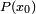
La méthode de Horner consiste à améliorer encore ce résultat en effectuant le calcul comme suit :
Le nombre de produits est alors réduit à n, de sorte que le temps de calcul d'une fonction polynomiale en un point a est seulement proportionnel au degré du polynôme. La méthode consiste donc à multiplier le premier coefficient par
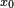
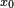
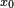
| Coefficients de P | an | an - 1 | an - 2 | ... | a1 | a0 |
| Facteur x0 | an | anx0 + an - 1 | (anx0 + an - 1)x0 + an-2 | ... | q0 | P(x0)=q0x0 + a0 |
Exemple pratique : Calcul de
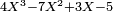
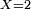
| Coefficients de P | 4 | − 7 | 3 | − 5 |
| Facteur 2 | 4 | 8 − 7 = 1 | 2 + 3 = 5 | P(2) = 10 − 5 = 5 |
Cette méthode permet aussi d'effectuer une conversion rapide d'un nombre écrit en base
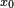
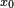
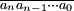
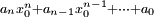
Exemple pratique : écriture en base 10 du nombre hexadécimal DA78
| Coefficients | 13 | 10 | 7 | 8 |
| Facteur 16 | 13 | 13 × 16 + 10 = 218 | 218 ×16+ 7 = 3495 | DA78 = 3495 × 16 + 8 = 55928 |