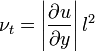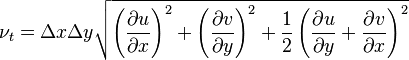Modélisation des turbulences - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La modélisation des turbulences est une branche de la modélisation de la dynamique des fluides où le modèle prend en compte sa dépendance par rapport au temps. Il y a beaucoup de modèles mathématiques pour comprendre la turbulence dans l'écoulement d'un fluide. L'écoulement d'un fluide est régit par les Équations de Navier-Stokes dans l'approximation des milieux continus. Ces équations sont non résolvable analytiquement à l'heure actuelle. Pour pallier ce problème plusieurs approches ont été faite dont celle de l'approximation de la couche limite.
Modélisation analytique
Joseph Boussinesq est le premier théoricien de ce domaine. Il introduit le concept de remous de viscosité. Dans ce modèle, une contrainte supplémentaire de turbulence est imposée en augmentant la viscosité d'un facteur supplémentaire nommé viscosité de remous. Cela va de la simple constante (qui fonctionne bien dans certaine modélisation 2D d'écoulement axis-métrique). Plus tard, Ludwig Prandtl introduit le concept de longueur variable le long de la couche limite. Pour un écoulement autour d'un mur, la viscosité de remous dans la couche limite doit varier avec la distance au mur en plus de la notion de « longueur variable ». Dans un simple modèle d'écoulement d'un fluide autour d'un mur, la viscosité de remous donne les équations suivantes :
- où:
-
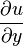
- l est la distance du mur (ou de l'obstacle).
Ce simple modèle est basé sur la « Loi du mur », est étonnamment précis quand la couche limite du mur a de petits gradients de pression.
Plus généralement les équations ont évolué avec le temps, pour se rapprocher d'une formulation type la théorie des champs similaire aux équations de Navier-Stokes .
Joseph Smagorinsky (1964) proposa un équation pratique pour la viscosité de remous en modélisation numérique, basée sur des variations locales du champ vitesse et une échelle locale de la discrétisation :
modélisation numérique
Les modélisations numériques peuvent être divisées en trois grandes catégories :
- L'approches statistiques ou Reynolds Averaged Navier-Stokes (RANS)
- La simulation numérique directe ou Direct Numerical Simulation (DNS)
- La simulation des grandes échelles ou Large Eddy Simulation (LES)
Ces deux dernières techniques concernent la simulation instationnaire et tridimensionnelle.
RANS
Cette méthode repose sur la décomposition de Reynolds autour de la Moyenne de Reynolds.
DNS
La simulation numérique directe a pour ambition de calculer toutes les échelles significatives de l’écoulement turbulent, i.e. jusqu’à la Dimension de Kolmogorov : il n’y a donc pas de problème de fermeture, mais l’algorithme numérique doit être suffisamment précis.
LES
La simulation des grandes échelles repose sur les équations de Navier-Stokes filtrées spatialement.