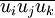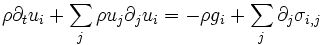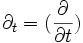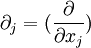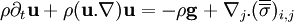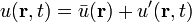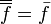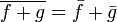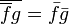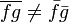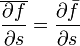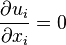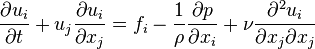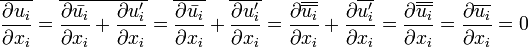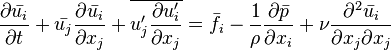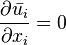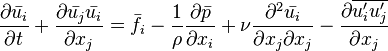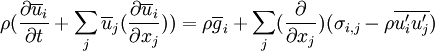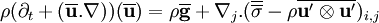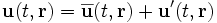Moyenne de Reynolds - Définition

Introduction

Dans le cadre du traitement en mécanique des fluides de la turbulence, l'utilisation de la décomposition de Reynolds appliquée aux solutions de l'équation de Navier-Stokes permet de simplifier le problème en faisant disparaitre les fluctuations de périodes et d'amplitudes courtes.

L'équation de Navier-Stokes

On rappelle la forme de l'équation de Navier Stokes dans le cas des fluides incompressibles:

avec les notations

ou encore sous une forme plus compacte:

où u_i(t,x_j)représente la ième composante du champ de vitesses instantanées à l'instant t aux coordonnées (x₁,x₂,x₃) dans le fluide, et représentent respectivement les dérivations partielles par rapport au temps et par rapport à la ième coordonnée spatiale, ρ représente la densité du fluide,ici constante d'après l'hypothèse d'incompressibilité et le tenseur des contraintes défini par ses composantes:

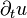
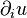
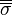
où δ_i,j vaut 1 si i=j et 0 sinon;

Moyenne de Reynolds et équation de Reynolds

Le principe repose sur la décomposition d'une variable entre sa moyenne et ses fluctuations, soit :

avec est le vecteur position,

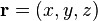
Or par définition la moyenne suit les règles suivantes :

et de même par définition , ce qui va simplifier les calculs.

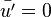
Les équations de la conservation de la matière (équation de continuité ) et de la quantité de mouvement sont :

En remplaçant les variables par la notion de moyenne

, etc.

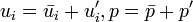
En moyennant les Équations de Navier-Stokes (ce qui a pour effet de faire disparaitre les termes de fluctuation rapides, qui sont de moyenne nulle), elles deviennent :

d'où :

Le même calcul plus général peut être mené avec le tenseur des contraintes σ_i,j au lieu de la viscosité ν. L'équation de Navier-Stokes devient l'équation de Reynolds :

ce qui peut encore s'écrire:

Il reste donc un terme fonction des fluctuations rapides, mais seulement par le truchement de leur variance, c’est-à-dire de la moyenne de leur carré qui en fait donc un terme sinon constant du moins variant peu. Dans le cadre de l'approximation hydrodynamique, ce terme est constant et est représenté par un tenseur: qui est appelé tenseur de Reynolds.

Décomposition de Reynolds

L'utilisation de la décomposition de Reynolds se justifie lorsqu'on a affaire à un phénomène présentant un spectre séparé en deux parties nettement distinctes: une bande de basses fréquences ou de régime quasi-permanent, de contribution moyenne sinon constante, du moins variant peu au cours du temps, nettement séparée d'une bande de régimes transitoires de haute fréquence et de contribution moyenne nulle. Ainsi:

où la barre au-dessus du u signale la moyenne glissante sur l'échelle choisie,l'apostrophe sur le u signale le terme d'écart par rapport à cette moyenne. Attention! Il ne s'agit pas forcément d'une perturbation! Cet artifice permet de découpler le problème du flux de base soumis à la viscosité turbulente, du problème de la turbulence elle-même.

Tenseur de Reynolds

• La demi-trace du tenseur de Reynolds s'identifie de façon évidente avec la densité de l'énergie cinétique;
• La partie non diagonale du tenseur de Reynolds peut être interprétée comme un terme de viscosité supplémentaire s'appliquant à l'écoulement moyen en s'ajoutant à la viscosité cinématique ν et baptisée viscosité turbulente
• Le tenseur de Reynolds obéit à une équation de transport, qui fait apparaître elle-même un terme de degré 3 en u :