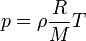Équations de Navier-Stokes - Définition
En mécanique des fluides, les équations de Navier-Stokes sont des équations aux dérivées partielles non-linéaires qui décrivent le mouvement des fluides dans l'approximation des milieux continus. Elles gouvernent par exemple les mouvements de l'air de l'atmosphère, les courants océaniques, l'écoulement de l'eau dans un tuyau, et de nombreux autres phénomènes d'écoulement de fluides. Elles sont nommées d'après deux physiciens du XIXe siècle, Claude Navier et George Stokes. Notons qu'il est possible de démontrer les équations de Navier-Stokes à partir de l'équation de Boltzmann.
Formule générale pour un fluide constitué d'une seule espèce chimique
Il existe bien des formes des équations de Navier-Stokes. Nous n'en présenterons que certaines. Il est à noter que ces formes dépendent aussi des notations utilisées. Ainsi, il existe plusieurs façons équivalentes d'exprimer les opérateurs différentiels.
La formulation différentielle de ces équations est la suivante :
- Équation de continuité (ou équation de bilan de la masse)
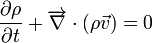
- Équation de bilan de la quantité de mouvement
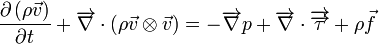
- Équation de bilan de l'énergie
![\frac{\partial \left( \rho e\right)}{\partial t} + \overrightarrow{\nabla} \cdot \left[ \; \left(\rho e + p\right) \vec{v} \; \right] = \overrightarrow{\nabla} \cdot \left( \overrightarrow{\overrightarrow {\tau}} \cdot \vec{v} \right) + \rho \vec{f} \cdot \vec{v} - \overrightarrow{\nabla} \cdot \vec{\dot{q}} + r](https://static.techno-science.net/illustrationWebp/Definitions/autres/e/e8a47959f3cb607b5049f19c0a99e93e_f51c6bbaa6353d59a72fb106a400ce4c.png)
Dans ces équations :
-
-
-
-
-
-
-
-
-
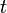
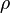
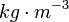
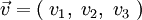
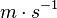
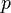
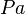
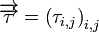
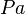
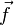
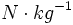
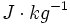
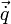
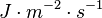
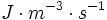
Remarques:
- L'énergie totale peut se décomposer en énergie interne u et en énergie cinétique selon
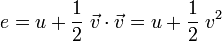
- L'opérateur nabla, en coordonnées cartésiennes, est un opérateur de dérivation spatiale du 1er ordre. Les opérateurs gradient, divergence et laplacien peuvent s'écrire à l'aide de cet opérateur :
-
-
-
-
-
-
-
-
-
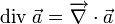
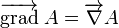
Expression en coordonnées cartésiennes
En coordonnées cartésiennes
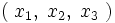
- Équation de continuité :
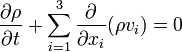
- Équation de bilan de la quantité de mouvement (j = 1,2,3)
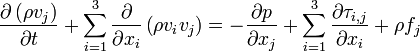
- Équation de bilan de l'énergie
![\frac{\partial \left( \rho e\right)}{\partial t} + \sum_{i=1}^3 \frac{\partial}{\partial x_i} \left[ \; \left(\rho e + p\right) v_i \; \right] = \sum_{i=1}^3 \sum_{j=1}^3 \frac{\partial}{\partial x_i}\left( \tau_{i,j} v_j \right) + \sum_{i=1}^3 \rho f_i v_i - \sum_{i=1}^3 \frac{\partial \dot{q}_i}{\partial x_i} + r](https://static.techno-science.net/illustrationWebp/Definitions/autres/3/36175c35e574dd1b15efad57adb0ad88_41f757799a6be3bcf4f14e0b4843cbb1.png)
Fluide newtonien, hypothèse de Stokes
En première approximation, pour de nombreux fluides usuels comme l'eau et l'air, le tenseur des contraintes visqueuses est proportionnel à la partie symétrique du tenseur des taux de déformation (hypothèse de Newton) et le flux de chaleur est proportionnel au gradient de la température (loi de Fourier), c'est-à-dire
-
![\overrightarrow{\overrightarrow {\tau}} = \mu \left[ \left( \overrightarrow{\nabla} \otimes \vec{v} \right) + \left( \overrightarrow{\nabla} \otimes \vec{v} \right)^t \right] + \eta \left( \overrightarrow{\nabla} \cdot \vec{v} \right) \; \overrightarrow{\overrightarrow {I}}](https://static.techno-science.net/illustration/Definitions/autres/4/4bfc87c7bc8aeeb3d94967dfc3563a2c_019bcbfe5bd588816429a6f43efed79d.png)
![\overrightarrow{\overrightarrow {\tau}} = \mu \left[ \left( \overrightarrow{\nabla} \otimes \vec{v} \right) + \left( \overrightarrow{\nabla} \otimes \vec{v} \right)^t \right] + \eta \left( \overrightarrow{\nabla} \cdot \vec{v} \right) \; \overrightarrow{\overrightarrow {I}}](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4bfc87c7bc8aeeb3d94967dfc3563a2c_019bcbfe5bd588816429a6f43efed79d.png)
-
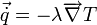
où :
-
-
-
-
-
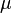
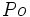
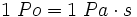
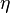
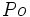
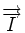
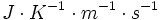
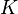
L'ensemble des fluides pour lesquels cette hypothèse est vérifiée sont appelés fluides newtoniens. On leur adjoint généralement l'hypothèse de Stokes :
-
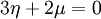
Cette hypothèse se révèle totalement fausse mais est couramment utilisée dans l'aéronautique.
Remarque :
De nombreux fluides, tels que les polymères, les hydrocarbures lourds, le miel, ou encore la pâte de dentifrice, ne vérifient pas ces hypothèses. La science chargée d'étudier les relations entre contrainte et déformation pour de tels fluides s'appelle la rhéologie.
Expression pour les écoulements de fluides compressibles
L'écoulement d'un fluide est dit incompressible lorsque l'on peut négliger ses variations de masse volumique au cours du temps. Cette hypothèse est vérifiée lorsque le nombre de Mach
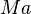
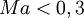
Pour un gaz parfait, cette équation d'état s'écrit
où
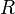
Expression pour les écoulements de fluides incompressibles
Pour un fluide visqueux newtonien et lorsque l'écoulement est incompressible, l'équation de l'énergie est découplée des équations de continuité et de quantité de mouvement, c'est-à-dire qu'on peut déterminer la vitesse et la pression indépendamment de l'équation de l'énergie. L'expression des équations de continuité et de quantité de mouvement sont considérablement simplifiées. On obtient alors
- Équation de continuité appelée alors équation d'incompressibilité
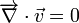
- Équation de bilan de la quantité de mouvement
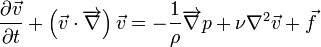
où
-
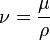
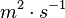
Interprétation
L'équation de quantité de mouvement est l'équivalent de la relation fondamentale de la dynamique (aussi appelée seconde loi de Newton) :
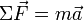
Dans cette formule, on voit apparaître trois types de forces :
- Les forces de pression, spécifique de la mécanique des fluides.
- Les forces de viscosité. Notez que le second terme contenant la viscosité de volume disparait si le fluide est incompressible.
- D'autres forces massiques, qui peuvent être des forces de gravité
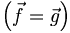
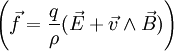
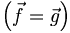
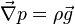
L'expression de l'accélération est plus délicate et s'exprime de deux manières
- L'approche lagrangienne consiste à suivre les particules de fluides. L'accélération est la dérivée particulaire de la vitesse:
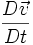
- L'approche eulérienne consiste à se placer en une position fixe. L'accélération est alors la somme de la dérivée
partielle de la vitesse
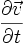
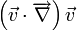
La résolution de l'équation de Navier-Stokes est extrêmement difficile. À la complexité inhérente aux équations aux dérivées partielles s'ajoutent celle de la non-linéarité introduite par le terme d'advection de l'accélération. La plupart du temps, on essaie de résoudre une version simplifiée de l'équation en éliminant l'un de ces termes. Par exemple, à faible nombre de Reynolds, on peut négliger le terme advectif (écoulement de Stokes) et à fort nombre de Reynolds, on s'affranchit de la viscosité (équation d'Euler).
Bibliographie
- Aérodynamique : Théories de la Dynamique des Fluides, A. Bonnet, J. Luneau, Éditions Cépaduès, septembre 89, 544 p.