Orbite de transfert - Définition

Introduction

Une orbite de transfert, dans le domaine de l'astronautique, est l'orbite sur laquelle est placé temporairement un véhicule spatial entre une orbite initiale, ou la trajectoire de lancement, et une orbite visée.

Le terme correspondant en anglais est transfer orbit.

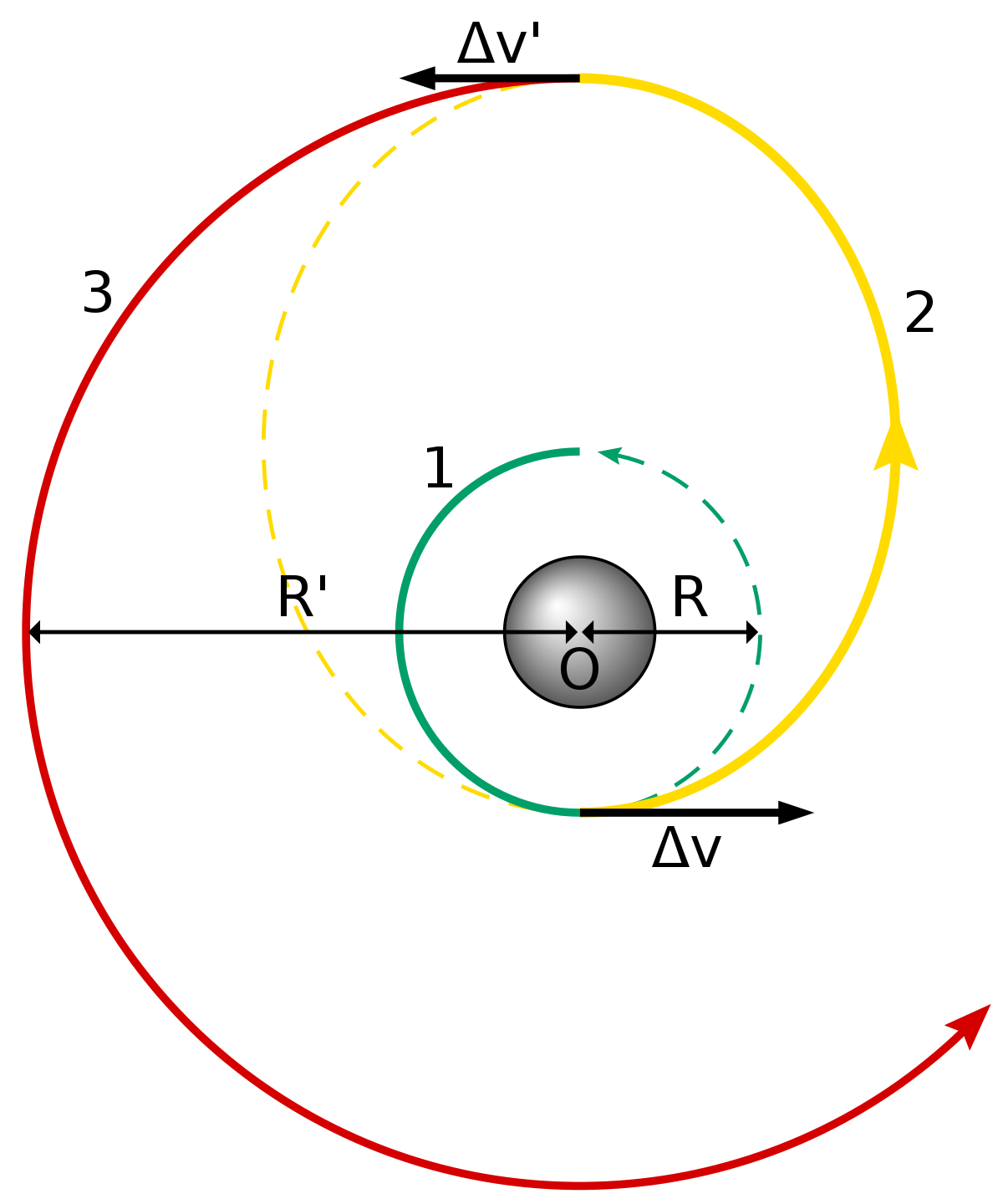
Orbite de transfert de Hohmann

Une trajectoire (ou transfert) de Hohmann est la trajectoire de moindre consommation d'énergie qui permet de passer d'une orbite à une autre. C'est aussi le plus lent des trajets possibles.

L'orbite de départ est circulaire de basse altitude, soit, par exemple, (avec R rayon terrestre), de période , de vitesse , dans laquelle et .

L'orbite visée est circulaire de haute altitude, soit, par exemple, , dont la période et la vitesse sont définies par des formules similaires.

L'orbite de Hohmann est l'ellipse de transfert de périgée et d'apogée , donc de grand axe , et d'excentricité . Son moment cinétique , son énergie et sa période sont donc connues.

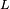
Au temps , le moteur fournit un surcroît de vitesse au satellite tel que . Au temps , le satellite parvient à son apogée mais avec une vitesse insuffisante. Le moteur fournit un surcroît de vitesse v' de sorte que .

Il faut donc que le décalage angulaire, au temps t₀, entre la position du satellite S₁ et la position du satellite S₂ soit , dans le cas d'un rendez-vous.

Le transfert du satellite de r₁ à r₂ entraîne un coût énergétique correspondant aux deux allumages du moteur : surcroît v = 0,277V₀, puis v' = 0,178V₀.