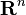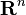Ouvert (topologie) - Définition
La liste des auteurs de cet article est disponible ici.
Exemples de définitions restreintes/corolaire pour des espaces particuliers
Topologies discrète et topologie grossière
Le caractère ouvert d'une partie d'un ensemble dépend de la topologie qu'on se donne. La plupart des espaces n'ont pas de topologie canonique, mais souvent plusieurs topologies intéressantes.
N'importe quel ensemble est ouvert, pour une topologie suffisamment fine, alors qu'une partie non triviale n'est pas ouverte pour une topologie trop grossière. Exemples :
- la topologie
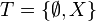
- l'ensemble
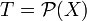
Espaces métriques
Soit (E,d) un espace métrique. Dans cet espace, une boule ouverte de centre
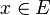
-
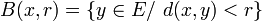
Une partie U de cet espace est ouverte si et seulement si pour tout point x de U, il existe une boule centrée sur x et incluse dans U :
De façon équivalente, U est ouverte si et seulement si tout point de U possède un voisinage inclus dans U.
Cela signifie que U est un ouvert de E si pour chacun de ses points x, il contient également les points suffisamment proches de x : on peut entourer chaque point en restant dans l'ouvert, donc aucun point deU n'est au bord de U.
Exemples :
- Toute boule ouverte est ouverte. Le nom de « boule ouverte » est donc cohérent avec la définition d'ouvert.
- L'ensemble vide et l'ensemble E sont des ouverts.
- La réunion et l'intersection de deux ouverts sont des ouverts.
Remarque :
- Dans



L'ensemble des ouverts de E est appelé la topologie de E.
Géométrie algébrique : ouverts de Zariski
En géométrie algébrique, un ensemble algébrique affine de
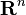
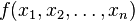
-
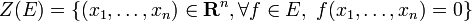
En particulier si f est un polynôme
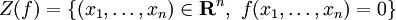
Remarque : si on prend pour E l'ensemble vide (aucun polynôme), on obtient :
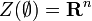
![E={\mathbf R}[X_1, X_2,\ldots X_n]](https://static.techno-science.net/illustration/Definitions/autres/8/83a4b02b0230b772b0e7c8ffd6b8b9b9_708c4027b4182e584619427ad9cddbc5.png)
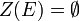
Les ensembles algébriques de
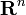
-
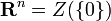
-
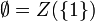
- une réunion finie
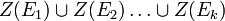
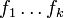
- une intersection (éventuellement infinie) d'ensembles algébriques {Z(Ei)}i est un ensemble algébrique Z(E) (avec
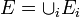
Il existe donc une unique topologie, appelée topologie de Zariski, sur
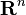
Les complémentaires dans
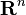
-
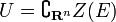
Les ouverts de la topologie de Zariski de la forme
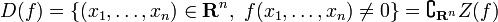
Exemple : Si n=1, les fermés sont R et les parties finies de R. Les ouverts sont l'ensemble vide et les ensembles
-
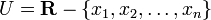
Ce sont des réunions finies d'intervalles ouverts. La topologie est aussi appelée topologie cofinie (pour complémentaires des ensembles finis).
Dans la théorie des schémas, on adopte une définition plus abstraite : les ouverts d'une topologie de Grothendieck (par exemple la topologie étale) sont définis comme des morphismes de certaines catégories.
Espaces vectoriels de dimension finie
Un espace vectoriel E de dimension finie sur un corps topologique K a une topologie canonique : il s'agit de la topologie la moins fine (ayant le moins d'ouverts) qui rende continues les formes linéaires (les fonctions linéaires de E dans K). Ainsi pour

Espaces euclidiens : définition basée sur la notion de point intérieur
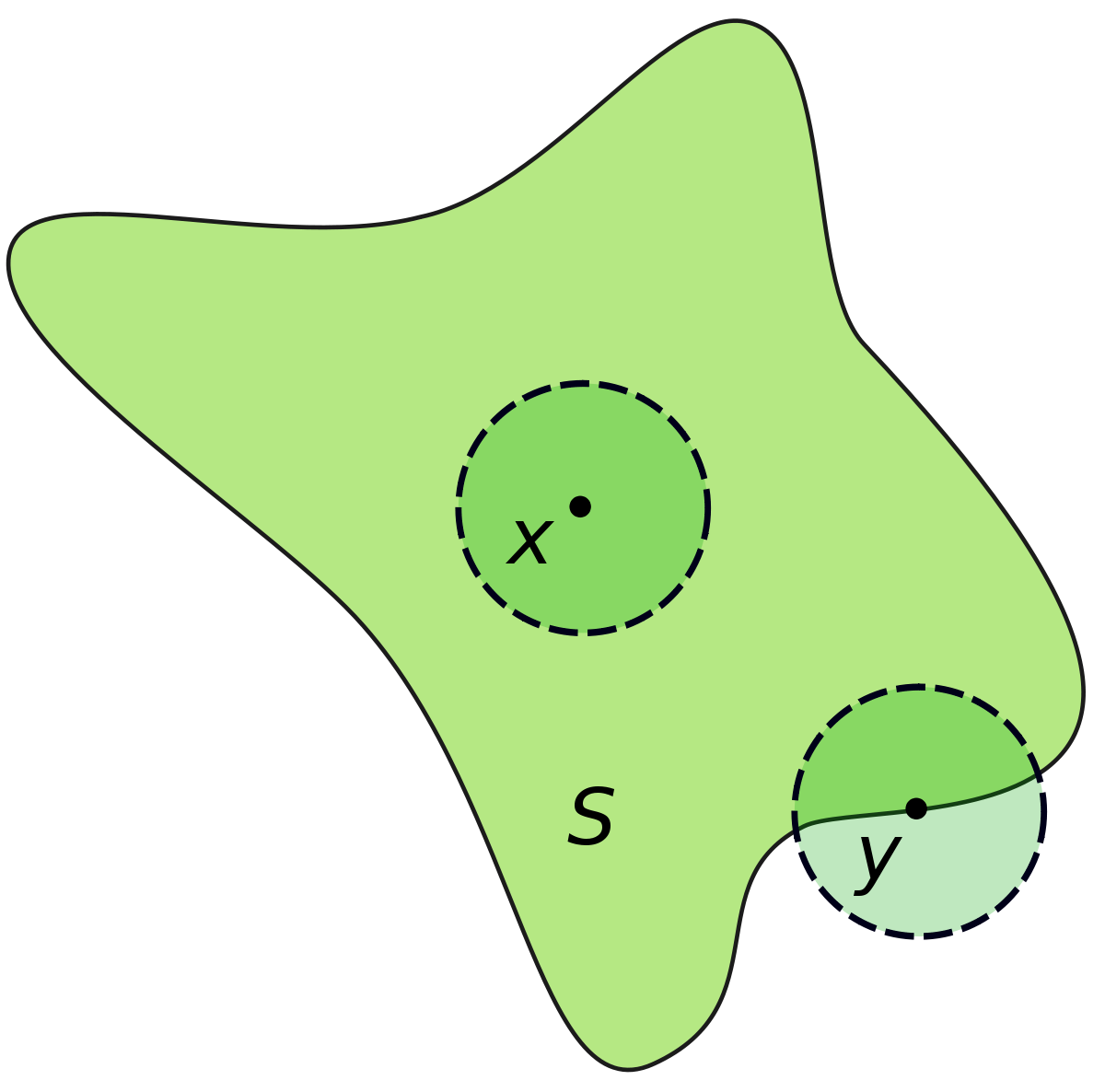
Si S est une partie d'un espace euclidien

Un sous-ensemble de points U de l'espace

- L'ensemble vide et l'ensemble
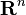
- La réunion et l'intersection de deux ouverts sont des ouverts.
L'ensemble des ouverts de