Ouvert (topologie) - Définition

Introduction

En mathématiques, et plus particulièrement en topologie générale, un ensemble ouvert, aussi appelé une partie ouverte ou, plus fréquemment, un ouvert, est un sous-ensemble d'un espace topologique qui ne contient aucun point de sa frontière. L'ouvert est l'élément de base d'une topologie. Il s'agit d'une notion fondamentale par sa transversalité dans presque tous les domaines des mathématiques.

Définitions

On définit un espace topologique par la donnée d'un couple (X,T) , où X est un ensemble et T sa topologie, c'est-à-dire un ensemble de parties de X () vérifiant les trois propriétés suivantes :

• et ,
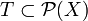
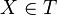
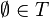
• T est stable par intersection finie : dès que et ,
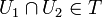
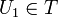
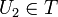
• T est stable par réunion quelconque : dès que tous les appartiennent à .

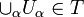
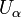
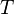
Par définition, un ensemble U est un ouvert de (X,T) si et seulement si U est un élément de T : la topologie est donc l'ensemble des ouverts.

De cette définition générale découlent des définitions corolaires restreintes aux espaces topologiques particuliers (couples ensembles/topologie) considérés.

Notamment les cas particuliers d'espaces topologiques les plus couramment étudiés:

• Espaces métriques
• Espaces Hilbertiens
• Espaces Hermitiens
• Espaces vectoriels normés
• Espaces Euclidiens

...

Intersection infinie d'ouverts

Une intersection infinie d'ouverts n'est pas nécessairement un ouvert.

Définitions associées

Fermé

Une partie d'un espace topologique (X,T) est fermée si son complémentaire dans X est un ouvert.

Intérieur d'une partie

Toute partie P d'un espace topologique (X,T) contient au moins un ouvert (éventuellement vide) ; le plus grand de ces ouverts est appelé l'intérieur de S. L'intérieur d'une partie est toujours défini est peut être construit en considérant l'union de tous les ouverts inclus dans S.

Voisinage d'une partie

Est appelé voisinage d'une partie A (non vide) d'une espace topologique E toute partie V de E contenant un ouvert U contenant A, c'est-à-dire tel que .

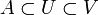
Les voisinages d'une partie non vide constituent un filtre, c'est-à-dire que l'intersection d'un nombre fini de voisinages est un voisinage et qu'une partie qui contient un voisinage est un voisinage.

Connexité

Un espace X est dit connexe si les seules parties ouvertes et fermées de X sont X et l'ensemble vide. Autrement dit, dans un espace connexe le complémentaire d'une partie ouverte n'est jamais un ouvert, sauf si la partie ou son complémentaire est vide.

Applications continues et parties ouvertes

Soit deux espaces topologiques E et F. Une fonction est continue si l'image réciproque de tout ouvert de F est un ouvert de E. Si c'est l'image directe d'un ouvert qui est ouverte, on parle d'application ouverte.

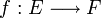
Intuition : ouverts de la droite et du plan

Exemple : Les points (x, y) qui satisfont à l'équation x² + y² = r² sont en bleu. Les points (x, y) qui satisfont à la relation x² + y² < r² sont en rouge. Les points rouges forment un ensemble ouvert. L'union des points bleus et rouges forme un ensemble fermé.

Un ensemble ouvert (appelé aussi ouvert) de la droite ou du plan est un ensemble qui est vide ou qui présente la caractéristique suivante : en choisissant comme origine un point quelconque de l'ensemble, tous les points autour de celui-ci sont encore dans l'ensemble à condition de ne pas trop s'éloigner. Cela signifie que ce point est assez loin de tous les points n'appartenant pas à l'ensemble, ou encore, qu'il existe toujours une distance non nulle entre ce point et le complémentaire de l'ensemble (les points n'appartenant pas à l'ensemble).

Exemple :

• Dans l'ensemble des nombres réels , l'intervalle X = ]0,1[, c'est-à-dire l'ensemble des réels x tels quel 0 < x < 1, est ouvert.
  Pour illustrer la définition, choisissons le point 0,99 (qui appartient à l'ensemble X). Tous les points à une distance de x inférieure ou égale à + 0,005 appartiennent encore à l'ensemble. En effet, tous ces réels y vérifient l'inégalité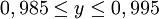 , et comme 0 < 0,985 et que 0,995 < 1, les réels y vérifient 0 < y < 1 et appartiennent bien à X. Pour démontrer que X est un ouvert, il faudrait faire le même raisonnement pour tous les points de X = ]0,1[, en ajustant au besoin la distance.

Contre-exemple :

• Dans l'ensemble des réels, l'intervalle Y = ]0,1], c'est-à-dire l'ensemble des nombres réels y tels que , n'est pas ouvert.
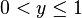
  En effet, si on choisit le point 1 (qui appartient à l'ensemble Y), il n'y a aucun point supérieur à 1 et appartenant à l'ensemble ]0,1], même si on s'éloigne très peu de ce point, dans le sens positif.

L'ensemble des ouverts de la droite (respectivement du plan) est appelé la topologie de la droite (respectivement la topologie du plan). On peut montrer que les ouverts de la droite sont l'ensemble vide et les ensembles qui sont réunion finie ou infinie d'intervalles ouverts.