Paramétrage - Définition

Généralisation

L'extension à p paramètres permet de formaliser la notion de variété de dimension p tracée dans un espace de dimension n. On reprend, mutatis mutandis les définitions de la dimension 2.

• quand l'application f a une différentielle injective (f est une immersion), on dit que la variété est immergée dans E. Ceci généralise la notion d'arc régulier, de nappe régulière. Et on peut alors définir le sous-espace tangent.

• il faut des contraintes supplémentaires pour que cette immersion devienne un plongement, permettant de parler de sous-variété de E.

Et de la même façon, il y a une notion de changement de paramétrage par difféomorphisme qui conserve les notions d'imersion, de sous-espace tangent.

Nappes paramétrées

Définition

Une nappe paramétrée de classe dans l'espace vectoriel E de dimension finie est la donnée

• d'un domaine U (en général supposé connexe) de ℝ² où variera le couple de paramétres réels (t,u)
• d'une fonction f de U dans E, de classe

Dans un repère donné de E, la fonction f a des composantes x(t,u),y(t,u),z(t,u)... Par exemple voici un paramétrage d'un cône de révolution de l'espace (parcouru plusieurs fois) : x(t,u)=u* cos (t),y(t,u)=u*sin(t),z(t,u)=u pour t,u variant dans ℝ.

Courbes tracées sur une nappe, plan tangent

Quand on se contente de faire varier un seul des deux paramètres, on obtient des arcs paramétrés tracés sur la nappe. Dans l'exemple du cône, si u varie seul avec t fixé on obtient une droite parcourue à vitesse uniforme. Si t varie avec u fixé, c'est un cercle.

Ces courbes permettent de définir la notion de plan tangent : on se place en (t₀,u₀), on regarde toutes les courbes tracées sur la surface et passant par ce point, et l'ensemble de leurs vecteurs tangents. S'ils forment un plan, c'est le plan tangent.

Une condition suffisante simple pour cela est que le point soit régulier, c'est-à-dire sont non colinéaires.

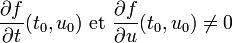
On peut aussi le dire sous la forme : un point est régulier quand la différentielle de f en ce point est injective.

Changement de paramètres

Le changement de paramètres sera cette fois un -difféomorphisme de U dans V autre domaine de ℝ². La notion de respect d'orientation sera liée cette fois au signe du jacobien de ce difféomorphisme.

On parlera de nouveau de nappes -équivalentes quand elles se correspondent par changement de paramétrage.

Les notions de point régulier, de plan tangent, d'aire, de courbure de Gauss font partie des invariants qu'on peut citer.