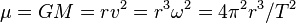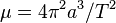Paramètre gravitationnel standard - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le paramètre gravitationnel standard d'un corps, noté
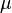
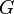
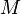
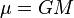
Le paramètre gravitationnel standard s'exprime en km3s-2 (kilomètre au cube par seconde au carré)
En astrophysique, ce paramètre fournit une simplification pratique des différentes formules liées à la gravitation.
Selon que
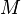
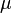
En fait, pour la Terre et le Soleil, ce produit
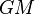
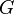
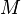
- Pour la Terre :
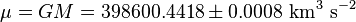
Petit objet en orbite stable
Si
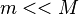
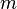
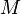
Le paramètre gravitationnel standard pertinent est relatif à la plus grosse masse
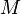
La troisième loi de Kepler permet de calculer le paramètre gravitationnel standard, pour toutes les orbites circulaires naturelles stables autour d'un même corps central de masse
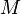
Orbites circulaires
Pour toutes les orbites circulaires autour d'un corps central :
avec :
-

-
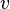
-
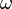
-
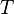
Orbites elliptiques
La dernière égalité ci-dessus relative aux orbites circulaires se généralise facilement aux orbites elliptiques :
où :
-
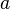
-
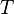
Trajectoires paraboliques
Pour toutes les trajectoires paraboliques
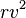
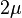
Pour les orbites elliptiques et paraboliques,
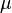
Valeurs de μ pour quelques corps célestes
Les valeurs de
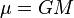
| Corps central | μ (km3s-2) | ||
|---|---|---|---|
| Soleil | 132 712 440 018 | ||
| Mercure | 22 032 | ||
| Vénus | 324 859 | ||
| Terre | 398 600 | ,4418 | ±0,0008 |
| Lune | 4902 | ,7779 | |
| Mars | 42 828 | ||
| Cérès | 63 | ,1 | ±0.3 |
| Jupiter | 126 686 534 | ||
| Saturne | 37 931 187 | ||
| Uranus | 5 793 939 | ± 13 | |
| Neptune | 6 836 529 | ||
| Pluton | 871 | ±5 | |
| Éris | 1 108 | ±13 | |