Phénomène de transfert - Définition

Nombres adimensionnels

Les nombres adimensionnels sont des nombres sans dimensions (unité = 1). Ils sont le résultat du produit ou rapport de grandeurs ayant une dimension, de telle façon que le rapport des unités équivaut à un.

Ces nombres sont largement utilisés en phénomème de transfert pour décrire le rapport entre 2 transferts et pouvoir ainsi caractériser le transfert de manière indépendante des conditions dans lesquelles ce dernier a lieu. Ainsi il devient possible de comparer 2 situations avec des éléments différents et des conditions différentes.

Nombres en transfert de chaleur

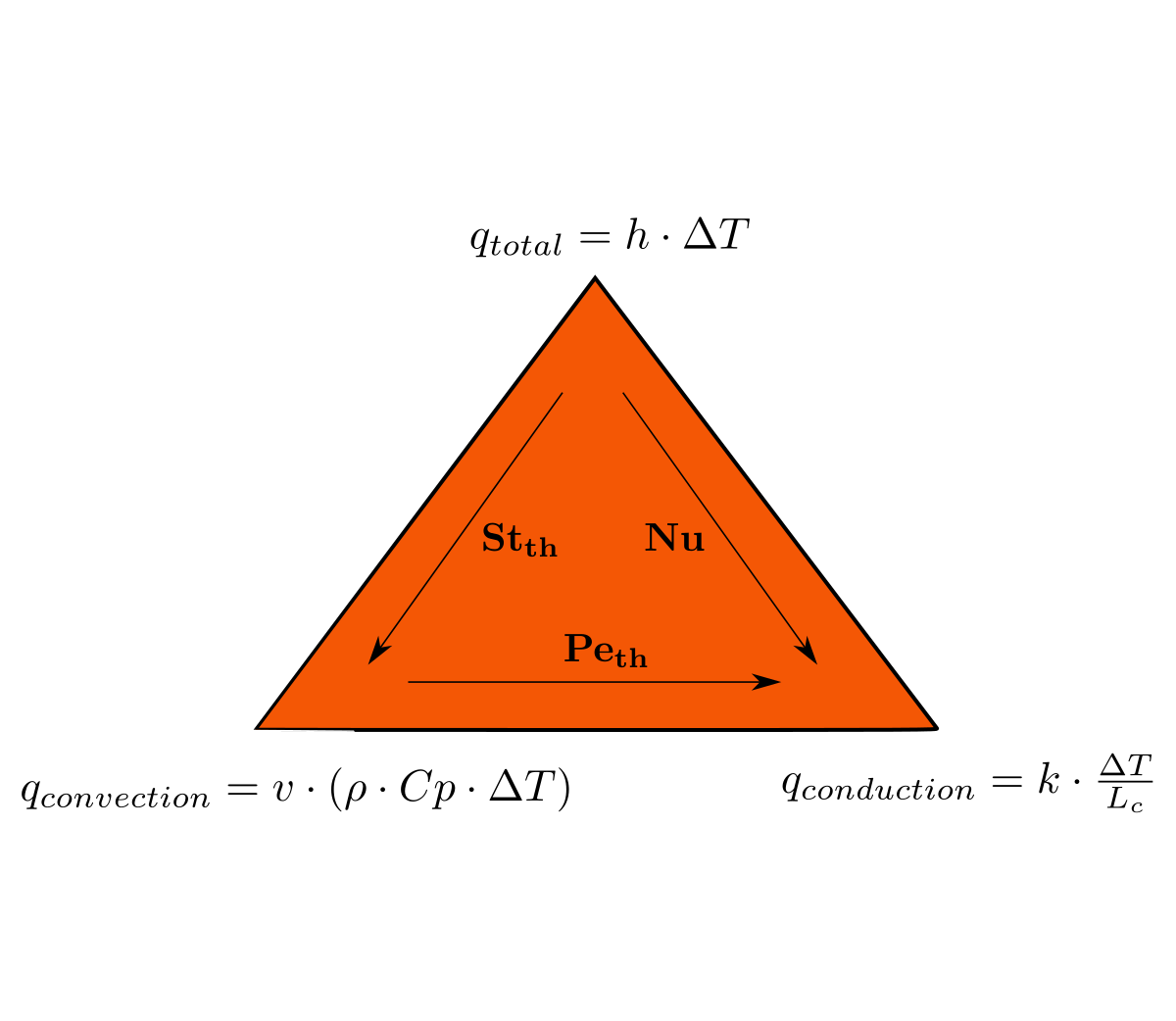
• Nombre de Nusselt:

Le nombre de Nusselt (Nu) correspond au rapport entre le transfert thermique total et le transfert thermique par conduction.

• Nombre de Peclet:

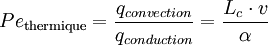
Le nombre de Peclet thermique (Pe_th) correspond au rapport entre le transfert thermique par convection et le transfert thermique par conduction.

• Nombre de Stanton:

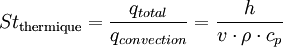
Le nombre de Stanton thermique (St_th) correspond au rapport entre le transfert thermique total et le transfert thermique par convection.

avec h le coefficient de transfert thermique, L_c la longueur caractéristique, k la conductivité thermique, α la diffusivité thermique et v la vitesse.

Nombres en transfert de masse

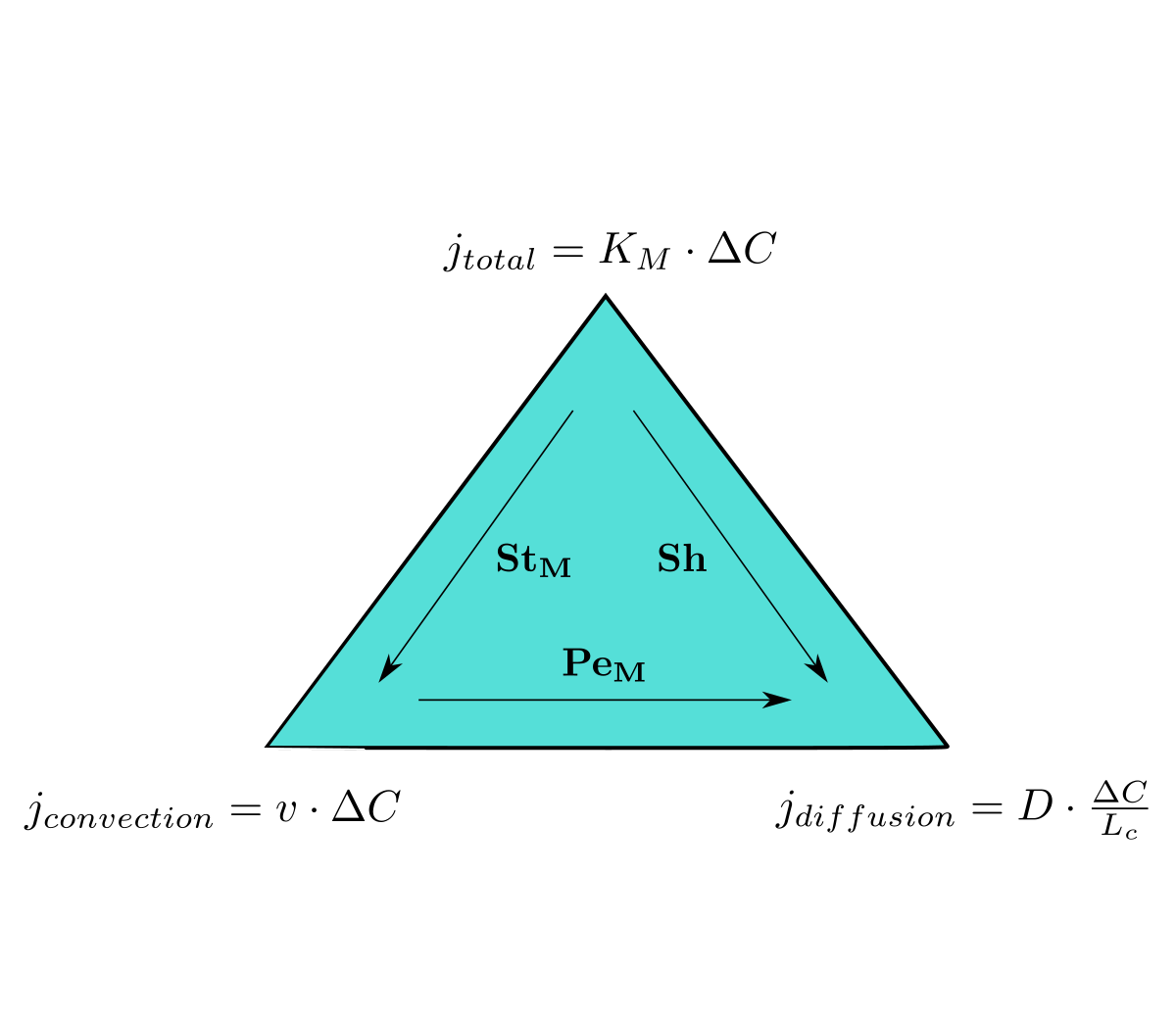
• Nombre de Sherwood:

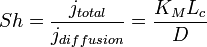
Le nombre de Sherwood (Sh) correspond au rapport entre le transfert massique total et le transfert de masse par diffusion.

• Nombre de Péclet:

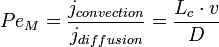
Le nombre de Peclet massique (Pe_M) correspond au rapport entre le transfert massique par convection et le transfert de masse par diffusion.

• Nombre de Stanton:

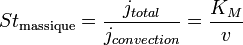
Le nombre de Stanton massique (St_M) correspond au rapport entre le transfert massique total et le transfert de masse par convection.

avec K_M le coefficient de transfert de masse, L_c la longueur caractéristique, D le coefficient de diffusion et v la vitesse.

Nombres en transfert simultané

Il s'agit de transferts mixtes: chaleur-masse, chaleur-quantité de mouvement, masse-quantité de mouvement.

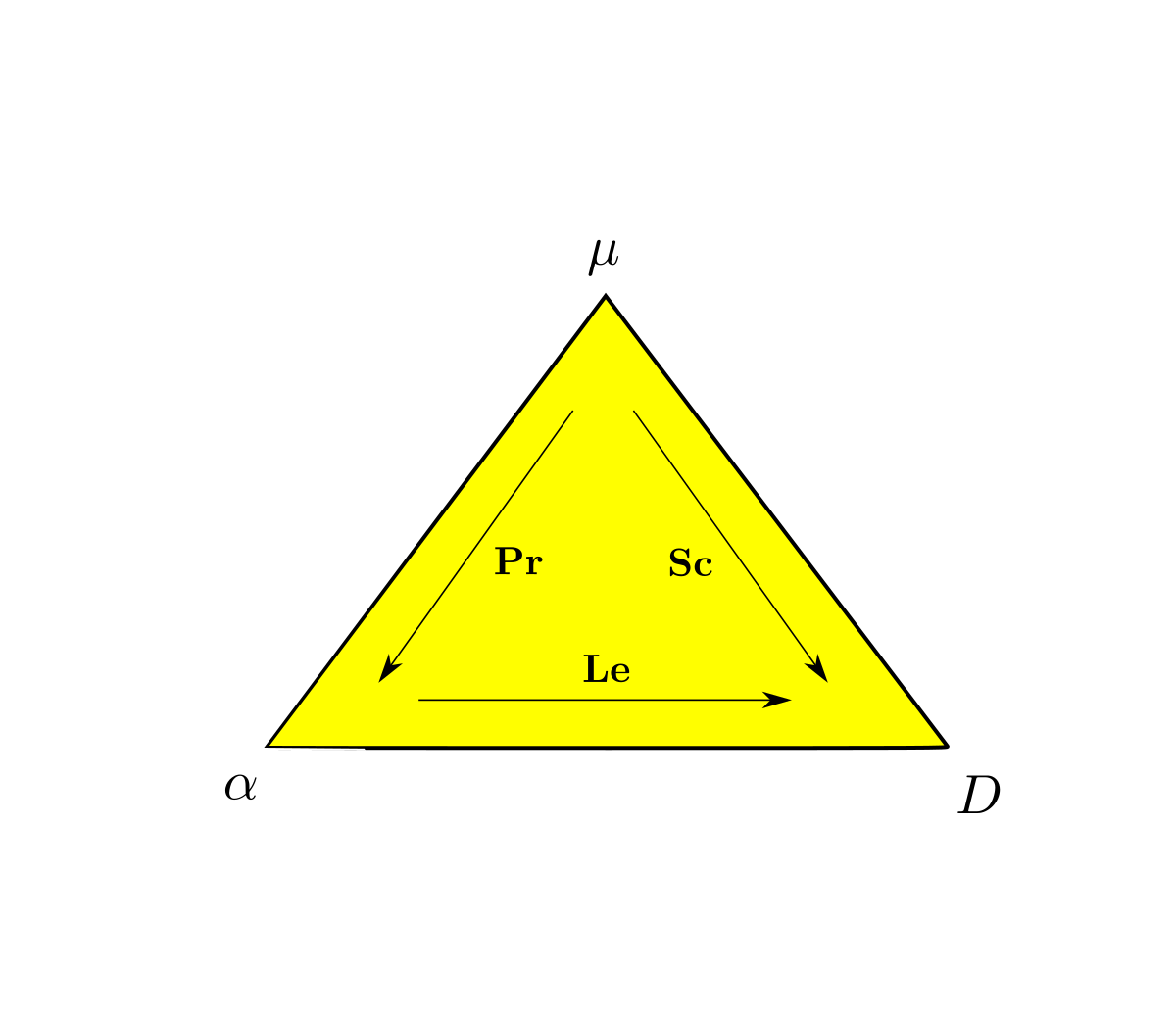
• Nombre de Prandtl:

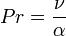
Le nombre de Prandtl (Pr) caractérise le transfert simultané de chaleur et de quantité de mouvement.

• Nombre de Schmidt:

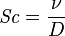
Le nombre de Schmidt (Sc) donne l'importance relative du transfert de masse et de quantité de mouvement.

• Nombre de Lewis:

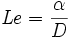
Le nombre de Lewis (Le) caractérise le transfert combiné de chaleur et de masse.

avec D le coefficient de diffusion, α la diffusivité thermique et ν la viscosité cinématique.