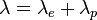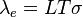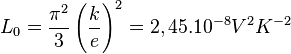Conductivité thermique - Définition

Introduction

La conductivité thermique est une grandeur physique caractérisant le comportement des matériaux lors du transfert thermique par conduction. Cette constante apparaît par exemple dans la loi de Fourier (voir l’article Conduction thermique). Elle représente la quantité de chaleur transférée par unité de surface et par une unité de temps sous un gradient de température de 1 degré par mètre.

Généralités

Dans le système international d’unités, la conductivité thermique est exprimée en watts par mètre par kelvin, (W·m^-1·K^-1) où :

• le watt est l’unité de puissance
• le mètre est l’unité de longueur (épaisseur/surface , m^-1 = m/m²)
• le kelvin est l’unité de température

La conductivité dépend principalement de :

• La nature du matériau,
• la température.

• D’autres paramètres comme l’humidité, la pression interviennent également.

En général, la conductivité thermique va de pair avec la conductivité électrique. Par exemple, les métaux, bons conducteurs d'électricité sont aussi de bons conducteurs thermiques. Il y a des exceptions, la plus exceptionnelle étant celle du diamant, qui a une conductivité thermique élevée (entre 1000 et 2 600 W·m^-1·K^-1) alors que sa conductivité électrique est basse.

D’un point de vue atomique, la conductivité thermique est liée à deux types de comportements :

• le mouvement des porteurs de charges, électrons ou trous.
• l’oscillation des atomes autour de leur position d’équilibre.

Dans les métaux, le mouvement des électrons libres est prépondérant alors que dans le cas des non-métaux, la vibration des ions est la plus importante.

La conductivité thermique est donc liée d’une part à la conductivité électrique (mouvement des porteurs de charge) et d'autre part à la structure même du matériau (vibrations des atomes). En effet dans un solide, les vibrations des atomes ne sont pas aléatoires et indépendantes les unes des autres, mais correspondent à des modes propres de vibration, aussi appelés « phonons » (on peut faire par exemple l’analogie avec un pendule ou une corde de guitare, dont la fréquence de vibration est fixée. Ces modes propres de vibration correspondent à des ondes qui peuvent se propager dans le matériau, si sa structure est périodique (organisée). Cette contribution sera donc plus importante dans un cristal, ordonné, que dans un verre, désordonné (d’où par exemple la différence de conductivité thermique entre le diamant ci-dessus et le verre dans le tableau).

Mathématiquement, la conductivité thermique λ peut donc s'écrire comme la somme de deux contributions :

où

• λ_e est la contribution des porteurs de charge (électrons ou trous)
• λ_p est la contribution des vibrations des atomes (phonons)

La contribution des porteurs de charge est liée à la conductivité électrique σ du matériau par la relation de Wiedemann-Franz :

où L est appelé « Facteur de Lorentz ». Ce nombre L dépend des processus de diffusion des porteurs de charge (ce qui correspond plus ou moins à la façon dont ils sont gênés par des obstacles lors de leurs déplacements, voir aussi diffusion des ondes) ainsi que de la position du niveau de Fermi. Dans les métaux, il est égal au nombre de Lorentz L₀, avec :

où

• k est la constante de Boltzmann
• e est la charge de l'électron