Postulats de la mécanique quantique - Définition

Formulation mathématique

La formulation mathématique de la mécanique quantique, dans son usage général, fait largement appel à la notation bra-ket de Dirac, qui permet de représenter de façon concise les opérations sur les espaces de Hilbert utilisés en analyse fonctionnelle. Cette formulation est souvent attribuée à John von Neumann.

Soit un espace séparable de Hilbert complexe. L'ensemble des états est l'espace projectif formé sur  ; autrement dit un état est une droite vectorielle (complexe) de . Un opérateur est une transformation linéaire d'un sous-espace dense de vers . Si cet opérateur est continu, alors cette transformation peut être prolongée de façon unique à une transformation linéaire bornée de vers . Par tradition, les choses observables sont identifiées avec des opérateurs, bien que ce soit discutable, particulièrement en présence des symétries. C'est pourquoi certains préfèrent la formulation d'état de densité.

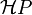
Dans ce cadre, le principe d'incertitude d'Heisenberg devient un théorème au sujet des opérateurs non-commutatifs. En outre, on peut traiter des observables continues et discrètes ; dans le premier cas, l'espace de Hilbert est un espace de fonctions d'onde de carré intégrables.