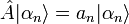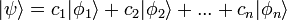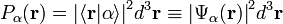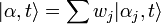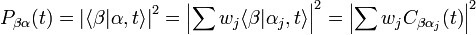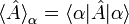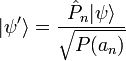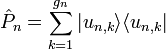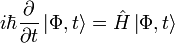Postulats de la mécanique quantique - Définition
La liste des auteurs de cet article est disponible ici.
Les postulats
Postulat I
Définition de l'état quantique
La connaissance de l'état d'un système quantique est complètement contenue, à l'instant t, dans un vecteur normalisable de l'espace des états


Postulat II
Principe de correspondance
À toute propriété observable, par exemple la position, l'énergie ou le spin, correspond un opérateur hermitien linéaire agissant sur les vecteurs d'un espace de Hilbert

Les opérateurs associés aux propriétés observables sont définis par des règles de construction qui reposent sur un principe de correspondance :
- L'opérateur de position
-
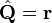
- L'opérateur d'énergie potentielle classique ou électromagnétique
-
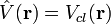
- L'opérateur de quantité de mouvement
-
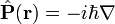

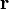
- L'opérateur de moment angulaire
-
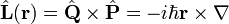
- L'opérateur d'énergie cinétique
-
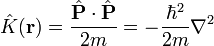
- L'opérateur d'énergie totale, appelé hamiltonien
-
- L'opérateur action du système, appelé lagrangien
-
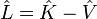
Postulat III
Mesure : valeurs possibles d'une observable
La mesure d'une grandeur physique représentée par l'observable A ne peut fournir que l'une des valeurs propres de A.
Les vecteurs propres et les valeurs propres de cet opérateur ont une signification spéciale : les valeurs propres sont les valeurs pouvant résulter d'une mesure idéale de cette propriété, les vecteurs propres étant l'état quantique du système immédiatement après la mesure et résultant de cette mesure (voir postulat V : réduction du paquet d'onde). En utilisant la notation bra-ket, ce postulat peut s'écrire ainsi :
où

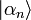
Les états propres de tout observable

Cela signifie que tout vecteur

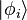
Postulat IV
Postulat de Born : interprétation probabiliste de la fonction d'onde
La mesure d'une grandeur physique représentée par l'observable A, effectuée sur l'état quantique normalisé

Le produit scalaire d'un état et d'un autre vecteur (qu'il appartienne ou non à

- Pour un système constitué d'une seule particule dans un état
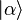
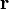
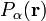
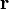
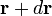
-
-
- Donc
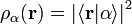
-
- Si le système est dans un état
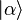
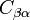
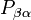
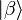
-
-
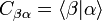
-
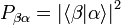
-
- Ni
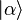
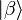
-
- Dans l'éventualité où un système peut évoluer vers un état
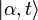
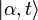
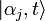
-
-
- où
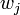
- L'amplitude
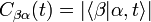
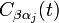
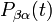
-
- Mais si une mesure a déterminé que le trajet k a été suivi, alors les coefficients deviennent
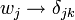
-
- En supposant que le système se trouve dans un état
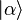

-
Postulat V
Mesure : réduction du paquet d'onde; obtention d'une valeur unique; projection de l'état quantique
Si la mesure de la grandeur physique A, à l'instant t, sur un système représenté par le vecteur

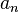
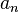
Où
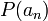
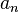
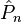
Avec
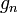
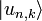
Ce postulat est aussi appelé "postulat de réduction du paquet d'onde".
Postulat VI
Évolution temporelle de l'état quantique
L'état
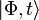
Le sixième postulat est l'équation de Schrödinger. Cette équation est l'équation dynamique de la mécanique quantique. Elle signifie simplement que c'est l'opérateur « énergie totale » du système ou hamiltonien, qui est responsable de l'évolution du système dans le temps. En effet, la forme de l'équation montre qu'en appliquant l'hamiltonien à la fonction d'onde du système, on obtient sa dérivée par rapport au temps c'est-à-dire comment elle varie dans le temps.
Cette équation n'est valable que dans le cadre non relativiste.