Problème de Josèphe - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques et en informatique, le problème de Josèphe ou problème de Joséphus est lié à certaines formulettes d'élimination. Il a été énoncé sous différentes formes, mais sa première formulation est due à Flavius Josèphe.
Description
Des soldats juifs, cernés par des soldats romains, décident de former un cercle. Un premier soldat est choisi au hasard et est exécuté, le troisième à partir de sa gauche (ou droite) est ensuite exécuté. Tant qu'il y a des soldats, la sélection continue. Le but est de trouver à quel endroit doit se tenir un soldat pour être le dernier. Josèphe, peu enthousiate à l'idée de mourir, parvint à trouver l'endroit où se tenir. Quel est-il ?
Ce problème de permutations peut être complexifié, par exemple en faisant varier le nombre de soldats à « sauter », en demandant une solution générale pour un nombre fixe de soldats ou en demandant un certain nombre de survivants.
Solution
La solution proposée est donnée pour chaque deuxième soldat tué (k = 2). Une solution pour le cas général est également donnée. Les deux s'effectuent de façon récursive.
Soit f(n) qui donne la position du survivant lorsqu'il y a n personne (et k = 2).
Lors du premier tour complet, tous les soldats aux positions paires sont exécutés. Au deuxième tour, le nouveau 2e est exécuté, puis le nouveau 4e, etc. Si le nombre initial de personnes est pair, alors le soldat à la position x au 2e tour est à la position 2x − 1 au 1er tour (peu importe la valeur de x). Donc, la personne à la position f(n) était auparavant à la position 2f(n) − 1. Cela nous permet de trouver la 1re formule de récurrence :
-
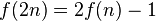
Si le nombre initial de soldats est impair, il vaut mieux voir le soldat à la position 1 comme exécuté à la fin du 1er tour. Pendant le 2e tour, le soldat à la 2e position est exécuté, puis le 4e, etc. Dans ce cas, le soldat à la position x était auparavant à la position 2x + 1. Cela nous permet de trouver la 2e formule de récurrence :
-
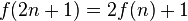
Les valeurs tabulées de n et f(n) font apparaître un schéma :
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| f(n) | 1 | 1 | 3 | 1 | 3 | 5 | 7 | 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 1 |
f(n) est une série de valeurs impaires croissantes qui recommence à 1 pour chaque puissance de 2.
Si nous choisissons m et l de façon à ce que n = 2m + l et
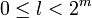
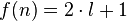
Théorème — Si
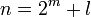
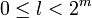

Le cas n = 1 est vrai. Analysons de façon séparée les cas n pair et n impair.
Quand n est pair, choisir
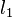
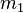

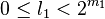
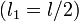
Nous avons
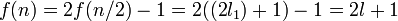
Quand n est impair, choisir
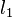
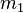
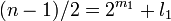

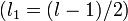
Nous avons
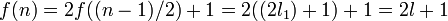
Pour le cas général, on peut faire appel à la programmation dynamique. Cette approche done la formule de récurrence :
Elle apparaît lorsque nous observons comment le nombre de survivants change en passant de n − 1 à n. Elle a un temps d'exécution asymptotique