Quadrique - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Applications
En modélisation d'image
Pour une surface d'équation
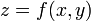
![\begin{align} p (x-a) + q (y-b) + \frac{1}{2} [r (x-a)^2 + 2 s (x-a)(y-b) + t (y-b)^2 ] \end{align}](https://static.techno-science.net/illustration/Definitions/autres/c/c470ab324077f8452a79819bca48cc83_937036e12d0dc2efb5d6adab38174bb2.png)
avec les notations dites de Monge
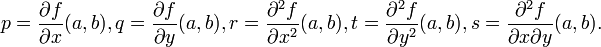
Cette approximation locale est exploitée en modélisation d'images, où elle fournit des résultats intéressants.

















































