Quadrivecteur - Définition

Quelques exemples de quadrivecteurs

• Quadrivecteur position-temps:

,

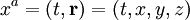
ou

.

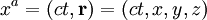
• Quadrivecteur vitesse (quadrivitesse) :

,

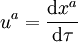
ou

,

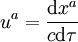
où τ est le temps propre, c'est-à-dire le temps qui serait indiqué par une horloge qui serait attaché à l'objet dont la trajectoire aurait le vecteur vitesse correspondant. Le quadrivecteur vitesse est par définition de norme fixée (par norme on entend la quantité η_abu^au^b, voir paragraphe ci-dessus), égale, selon la convention de coordonnée et de signe choisie à c², -c², 1, ou -1. La composante temporelle du quadrivecteur vitesse est déterminée par la condition que la norme soit égale à la valeur imposée.

• Quadrivecteur impulsion (quadri-impulsion). Pour une particule de masse non nulle :

,

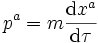
ou

,

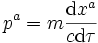
où τ est le temps propre. Le quadrivecteur impulsion possède une norme fixée, égale, selon la convention de coordonnée et de signe choisie à m²c², -m²c², m², ou -m². La composante temporelle du quadrivecteur vitesse est déterminée par la condition que la norme soit égale à la valeur imposée. On peut montrer qu'elle s'identifie (à une constante près) à l'énergie de l'objet telle qu'elle serait mesurée par un observateur immobile par rapport aux coordonnées x, y, z.

• Potentiel vecteur A^a. Ce quadrivecteur potentiel est défini avec des composantes contravariantes. Ses composantes spatiales s'identifient (au signe près) au potentiel vecteur de l'électromagnétisme, dont le rotationnel donne le champ magnétique. Sa composante temporelle donne, à un facteur multiplicatif près, le potentiel électrique.

• nabla: est un opérateur covariant. Ses composantes spatialles s'identifient (au signe près) au gradiant et sa composante temporelle s'identifie à la dérivée temporaile (à une constance 1/c) près. Sa pseudonorme s'identifie au d'alembertien