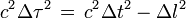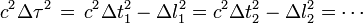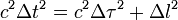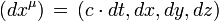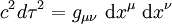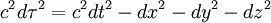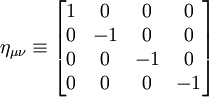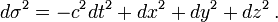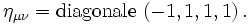Temps propre - Définition

Introduction

En théorie relativiste, on appelle temps propre d'une particule le temps mesuré dans le repère de cette particule, c'est-à-dire dans le repère où elle est immobile.

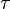
En relativité restreinte, l'intervalle de temps propre séparant deux événements est l'intervalle de temps les séparant dans un référentiel inertiel où ils ont lieu au même endroit de l'espace.

Définition et propriétés

En mécanique newtonienne on décrit le mouvement d'un corps dans un espace absolu par rapport à un temps absolu. Dans ce cadre la position d'un mobile, mesurée par ses coordonnées spatiales (x, y, z) dans un certain repère, est donnée en fonction du temps t. La théorie de la relativité déclare qu'il n'existe pas de temps absolu et que ce temps ne peut pas être séparé de l'espace. Elle raisonne sur des événements, chaque événement étant caractérisé par un lieu M et un instant t. Quand on suit des événements attachés à un corps libre en mouvement, on parle de ligne d'univers.

Considérons un vaisseau spatial se déplaçant librement dans l'espace, c'est-à-dire en ayant coupé tous ses moteurs (c'est donc un référentiel inertiel). Imaginons qu'il émette des éclairs à intervalles réguliers en accord avec une horloge située dans l'habitacle (cette horloge donne ce que l'on appelle le temps propre de la fusée). Appelons Δτ cet intervalle temporel local entre deux éclairs successifs ainsi mesuré. Puis considérons un autre référentiel inertiel depuis lequel d'autres observateurs voient passer devant eux la fusée à vitesse constante. Ces observateurs auront synchronisé leurs horloges et observeront les éclairs émis par la fusée quand elle passe devant eux en notant l'heure. Dans ce deuxième référentiel inertiel l'intervalle entre deux éclairs (deux événements) est caractérisé par deux nombres : la distance spatiale Δl observée entre les deux endroits où avaient lieu les éclairs et la distance temporelle Δt entre eux.

Une conséquence des axiomes d'Einstein, utilisable d'ailleurs comme principe pour fonder la relativité restreinte, est que l'on a l'égalité

et bien sûr le carré c²Δτ² est indépendant du référentiel d'observation choisi du fait qu'il ne dépend que de ce qui se passe dans la fusée. Autrement dit, tous les observateurs s'accordent sur la valeur de Δτ² ainsi calculée, bien que les valeurs de Δl et de Δt différent d'un système de repérage à l'autre. Donc dans différents référentiels inertiels numérotés 1, 2, ..., on a :

Puisque

le laps de temps observé Δt entre les deux éclairs mesuré dans un référentiel extérieur est toujours plus grand que la durée propre Δτ. Ainsi le temps écoulé entre deux événements donnés se produisant dans la fusée est toujours plus petit que celui mesuré à l'extérieur par les horloges du dehors de l'autre référentiel coïncidant avec les éclairs au moment où ils sont émis. Ce phénomène de ralentissement des horloges est illustré par le célèbre paradoxe des jumeaux.

Formulation tensorielle

Le tenseur de métrique permet de calculer la distance élémentaire entre deux événements voisins E1 et E2. Dans un repère donné le vecteur joignant E1 à E2 a pour coordonnées

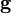
où μ est un indice à quatre valeurs 0, 1, 2, 3.

Dans un repère lorentzien le carré du temps propre est donnée par l'expression

et en identifiant avec la formule

on trouve immédiatement que le tenseur représente la métrique de Minkowski

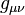
En changeant tous les signes il est courant aussi d'utiliser le carré de la distance spatiale dσ² entre les deux événements, plutôt que le carré de la distance temporelle c²dτ². La première quantité est donc donnée par

Dans le premier cas (carré d'un intervalle temporel) on parle de la signature

et dans le second (carré d'un intervalle spatial), de la signature