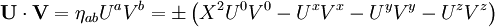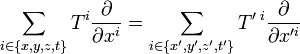Quadrivecteur - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Quadrivecteurs covariants et contravariants - Quelques exemples de quadrivecteurs

Introduction

La théorie de la relativité (restreinte, puis générale) postulée par Einstein amène à considérer les trois coordonnées d'espace (par exemple hauteur, largeur, profondeur) et le temps comme formant un tout indissociable. Un quadrivecteur est alors :

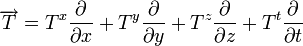
un vecteur $\overrightarrow{T} = T^x\frac{\partial}{\partial x} + T^y\frac{\partial}{\partial y} + T^z\frac{\partial}{\partial z} +T^t\frac{\partial}{\partial t}$ tangeant à l'espace-temps modélisé comme une variété différentielle de dimension 4 ;
observé dans un référentiel R, dont (x,y,z,t) est un repère ;
invariant quand on passe d'un référentiel galiléen à un autre.

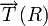
Autrement dit, un quadrivecteur est une fonction $\overrightarrow{T}(R)$ du référentiel d'observation, et on demande à cette fonction d'être constante sur l'ensemble des référentiels galiléens. Si R et R' sont 2 référentiels galiléens cela s'écrit

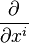
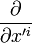
En relativité restreinte le changement de référentiel galiléen se fait par une transformation de Lorentz. Le passage des vecteurs de base $\frac{\partial}{\partial x^i}$ aux $\frac{\partial}{\partial x'^i}$ se fait par une transformation de Lorentz ; les coordonnées $T\, ^i$ du quadrivecteur doivent par conséquent également suivre une transformation de Lorentz pour compenser le changement de base et assurer l'égalité plus haut. C'est ce que l'on nomme covariance des coordonnées d'un quadrivecteur.

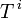
Quadrivecteurs covariants et contravariants

Un quadrivecteur peut exister sous deux formes, dites covariante et contravariante. La distinction entre ces deux formes se fait à l'aide de la position des indices des composantes de quadrivecteurs.

Quand les indices sont notés en exposant, on parle d'indices covariants. Quand ils sont notés en bas, on parle d'indices contravariants. Par exemple, pour un vecteur V :

Les V^a sont les composantes contravariantes du vecteur,
Les V sont les composantes covariantes du vecteur.

Dans chacun des cas le symbole a est supposé décrire l'ensemble des symboles des coordonnées du quadrivecteur.

Les coordonnées x, y, z et t sont des quantités covariantes. On les note ainsi sous la forme

(t, x, y, z) = x a

Il est possible de passer de la forme covariante à la forme contravariante des composantes d'un vecteur à l'aide d'une opération qui peut formellement s'assimiler à une multiplication matricielle, à l'aide d'une matrice symétrique en général notée η. On a ainsi, pour tout vecteur

V_a =	∑	η_abV^b.
	b

Dans ce genre de sommation, il est de coutume d'omettre le signe somme, celle-ci étant implicite chaque fois qu'un indice apparait simultanément en haut et en bas dans une formule (c'est la convention d'Einstein). L'équation précédente se note ainsi

V a = η a b V b

La transformation inverse se fait à l'aide de la matrice inverse, notée avec des indices en haut,

On a ainsi

V a = η a b V b

La matrice η est appelée métrique de Minkowski. Sa forme matricielle dépend du système de coordonnée choisi. Dans le cas où l'on se place en coordonnées cartésiennes, elle s'écrit

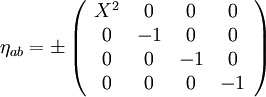
\eta_{ab} = \pm \left(\begin{array}{cccc} X^2 & 0 & 0 & 0\\ 0 & - 1 & 0 & 0\\ 0 & 0 & -1 & 0\\ 0 & 0 & 0 & -1\end{array} \right)

La quantité X vaut c (la vitesse de la lumière) ou 1 selon que la coordonnée temporelle a été prise égale à t ou c t. Le signe de η est indéterminé, et dépend d'une convention arbitraire, appelée convention de signe de la métrique.

En règle générale, un quadrivecteur est défini de façon non ambiguë par sa forme covariante ou contravariante, l'autre forme étant déduite par l'action de la matrice η.

La matrice η permet de calculer la norme d'un quadrivecteur, ou plus généralement le produit scalaire entre deux vecteur. On a ainsi