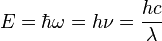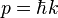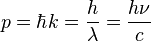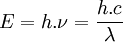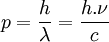Photon - Définition
| Photon | |
|---|---|
 Photons émis dans le faisceau cohérent d'un laser |
|
| Propriétés générales | |
| Composition | Elémentaire |
| Classification | Boson |
| Propriétés physiques | |
| Masse | 0 |
| Charge | 0 |
| Spin | 1 |
| Durée de vie | Stable |
| Historique | |
En physique des particules, le photon est la particule élémentaire médiatrice de l'interaction électromagnétique. Autrement dit, lorsque deux particules chargées électriquement interagissent, cette interaction se traduit d'un point de vue quantique comme un échange de photons. Dans la conception actuelle de la lumière, les ondes électromagnétiques, des ondes radio aux rayons gamma en passant par la lumière visible, sont toutes constituées de photons.
Le concept de photon a été développé par Albert Einstein entre 1905 et 1917 pour expliquer des observations expérimentales qui ne pouvaient être comprises dans le cadre d'un modèle ondulatoire classique de la lumière.[1][2][3][4] Il a ainsi montré que parallèlement à ses propriétés ondulatoires – interférences et diffraction –, le champ électromagnétique présente simultanément des propriétés corpusculaires. Les photons sont des " paquets " d'énergie élémentaires ou quanta de rayonnement électromagnétique qui sont échangés lors de l'absorption ou de l'émission de lumière par la matière. De plus, l'énergie et la quantité de mouvement (pression de radiation) d'une onde électromagnétique monochromatique sont égales à un nombre entier de fois celles d'un photon.
Le concept de photon a donné lieu à des avancées importantes en physique expérimentale et théorique, telles que les lasers, les condensats de Bose-Einstein, l'optique quantique, la théorie quantique des champs et l'interprétation probabiliste de la mécanique quantique. Le photon est une particule de masse nulle et de spin égal à 1, c'est donc un boson[5]. On utilise généralement le symbole γ (gamma) pour le désigner.
L'énergie d'un photon de lumière visible est de l'ordre de 2eV, soit ~109 fois moins que l'énergie nécessaire pour créer un atome d'hydrogène. En conséquence, les sources de rayonnement habituelles (antennes, lampes, laser, etc.) produisent de très grandes quantités de photons[6], ce qui explique que la nature "granulaire" de l'énergie lumineuse soit négligeable dans de nombreuses situations physiques. Il existe cependant des processus permettant de produire des photons un par un :
- transition électronique ;
- transition nucléaire ;
- annihilation de paires particule-antiparticule.
Historique
Origine du terme "photon"
Les photons ont originellement été appelés " quanta de lumière " (das Lichtquant) par Albert Einstein.[1] Le nom moderne " photon " est derivé du mot grec qui signifie lumière, φ?ς, (translittéré phos), et a été choisi en 1926 par le chimiste Gilbert N. Lewis, dans la publication d'une théorie spéculative[7] dans laquelle les photons étaient " incréables et indestructibles ". Bien que la théorie de Lewis ne fut jamais acceptée, étant contredite par plusieurs expérimentations, son nouveau nom, photon, fut adopté immédiatement par la communauté scientifique.
En physique, un photon est représenté par le symbole 
, la lettre grec gamma. L'utilisation de ce symbole pour le photon provient probablement des rayons gamma, qui furent découverts et nommés en 1900 par Paul Ulrich Villard[8][9]. En 1914, Rutherford et Edward Andrade[10] démontraient que ces rayons gamma étaient une forme de lumière. En chimie et en optique, les photons sont habituellement symbolisés par 
, l'énergie du photon, où 
est la constante de Planck et la lettre grec 
(nu) est la fréquence du photon. À l'occasion, le photon peut être symbolisé par hf, où sa fréquence est identifié par f.
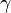
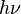
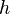
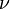
Développement de la notion de " quanta de lumière "
La description de la lumière a suivi a cours de l'histoire un curieux mouvement de balancier entre une vision corpusculaire et une vision ondulatoire. Dans la plupart des théories jusqu'au XVIIIe siècle, on considère que la lumière est constituée de particules. Bien que des modèles ondulatoires soient proposés par René Descartes (1637),[11] Robert Hooke (1665),[12] et Christian Huygens (1678),[13] les modèles particulaires restent dominants, en partie en raison de l'influence d'Isaac Newton.[14] Un changement de paradigme a lieu à partir de la mise en évidence des phénomènes d'interférences et de diffraction de la lumière par Thomas Young et Augustin Fresnel au début du XIXe siècle, et vers 1850 les modèles ondulatoires deviennent la règle.[15] La prédiction par Maxwell en 1865 du fait que la lumière soit une onde électromagnétique,[16] suivie de la confirmation expérimentale de Hertz en 1888,[17] semblent porter un coup de grâce aux théories corpusculaires de la lumière.
La théorie ondulatoire de Maxwell ne rend cependant pas compte de toutes les propriétés de la lumière. Cette théorie prédit que l'énergie d'une onde lumineuse dépend seulement de l'amplitude de l'onde, mais pas de sa fréquence ; or de nombreuses expériences indiquent que l'énergie transférée de la lumière aux atomes dépend seulement de la fréquence et non de l'amplitude. Par exemple, certaines réactions chimiques ne sont possible qu'en présence d'une onde lumineuse de fréquence suffisante : en dessous d'une fréquence seuil, quelque soit l'intensité incidente, la lumière ne peut amorcer la réaction. De manière similaire, dans l'effet photoélectrique les électrons ne sont éjectés d'une plaque de métal qu'au dessus d'une certaine fréquence, et l'énergie des électrons émis dépend de la fréquence de l'onde, et non de son amplitude. Dans le même ordre d'idée, les résultats obtenus à la fin du XIXe et au début du XXe siècle sur le rayonnement du corps noir[18] sont reproduits théoriquement par Max Planck en 1900 en supposant que que la matière interagissant avec une onde électromagnétique de fréquence ν ne peut reçevoir ou émettre de l'énergie électromagnétique que par paquets de valeur bien déterminée égale à hν – ces paquets étant appelés des quanta.[19][20]
Puisque les équations de Maxwell autorisent n'importe quelle valeur de l'énergie électromagnétique, la plupart des physiciens pensent initialement que cette quantification de l'énergie échangée est due à des contraintes encore inconnues sur la matière qui absorbe ou émet la lumière. En 1905, Einstein est le premier à proposer que la quantification de l'énergie soit une propriété de la lumière elle-même.[1] Bien qu'il ne remette pas en cause la validité de la théorie de Maxwell, Einstein montre que la loi de Planck et l'effet photoélectrique pourraient être expliqués si l'énergie de l'onde électromagnétique était localisée dans des quanta ponctuels qui se déplaçaient indépendemment les uns des autres, même si l'onde elle-même était étendue continuement dans l'espace.[1] Dans son article, Einstein prédit que l'énergie des électrons émis lors de l'effet photoélectrique dépend linéairement de la fréquence de l'onde. Cette prédiction forte sera confirmée expérimentalement par Robert Millikan en 1916, ce qui lui vaudra – parallèlement à ses expériences sur les gouttes chargées – le prix Nobel de 1923.[21] En 1909[2] et en 1916,[4] Einstein montre que, si la loi de Planck du rayonnement du corps noir est exacte, les quanta d'énergie doivent également transporter une impulsion p = h / λ, ce qui en fait des particules à part entière. L'impulsion du photon a été mise en évidence expérimentalement par Arthur Compton,[22] ce qui lui valut le prix Nobel de 1927.
Objections à l'hypothèse des quanta de lumière
Pendant tout le début de XXe siècle cependant, la notion de photon reste discutée, principalement en raison de l'absence d'un formalisme permettant de combiner les phénomènes ondulatoires avec les phénomènes corpusculaires nouvellement découverts. Ainsi en 1913, dans une lettre de recommandation en faveur de l'admission d'Einstein à l'académie des sciences de Prusse, Planck écrit[23] :
- Il ne faut pas trop lui tenir rigueur de ce que, dans ses spéculations, il ait occasionnellement pu dépasser sa cible, comme par exemple avec son hypothèse des quanta de lumière.
De nombreux effets mettant en évidence la nature quantifiée de la lumière peuvent en fait être également expliqués par une théorie semiclassique, dans laquelle la matière est quantifiée mais la lumière est considérée comme un champ électromagnétique classique. Parmi les phénomènes ainsi explicables, on peut par exemple citer l'existence d'un seuil dans l'effet photoélectrique, la relation entre l'énergie de l'électron émis et la fréquence de l'onde, le regroupement des photoélectrons dans un interféromètre Hanbury Brown et Twiss, ainsi que la statistique poissonienne des comptes.[24] Contrairement à une idée répandue, l'effet photoélectrique n'est donc pas la preuve absolue de l'existence du photon (bien que certaines expériences sur l'effet photoéléctrique ne puissent cependant pas être expliquées par une théorie semiclassique[24]).
L'expérience de Compton donne une existence plus tangible au photon, puisque ce dernier montre que la diffusion des électrons par les rayons X s'explique bien en attribuant au photon le moment cinétique prédit par Einstein. Cette expérience marque une étape décisive, après laquelle l'hypothèse des quanta de lumière emporte l'adhésion de la majorité des physiciens.[21] Dans une dernière tentative de sauver la variation continue de l'énergie électromagnétique et de la rendre compatible avec les expériences, Bohr, Kramers et Slater développent un modèle basé sur deux hypothèses drastiques[25] :
- L'énergie et l'impulsion ne sont conservées qu'en moyenne, mais pas lors des processus élémentaires tels que l'absorption et l'émission de lumière. Cela permet de réconcillier le changement discontinu de l'énergie de l'atome avec les variations continus de l'énergie de la lumière.
- La causalité est abandonnée. Par exemple, l'émission spontanée est simplement une émission induite par un champ électromagnétique "virtuel".
Cependant, des expériences de diffusion Compton plus précises montrent que l'énergie et l'impulsion sont conservées extraordinairement bien lors des processus élémentaires, et également que le recul de l'électron et la génération d'un nouveau photon lors de la diffusion Compton obéissent à la causalité à moins de 10ps près. En conséquence, Bohr et ses collaborateurs donnent à leur modèle "des funérailles aussi honorables que possible".[26] Sur le front théorique, l'électrodynamique quantique inventée par P.A.M. Dirac parvient à donner une théorie complète du rayonnement – et des électrons – expliquant la dualité onde-corpuscule. Depuis cette époque, et notamment grâce à l'invention du laser, les expériences confirment de manière de plus en plus directe l'existence du photon et l'échec des théories semiclassiques.[27] Il est notamment devenu possible de mesurer la présence d'un photon sans l'absorber, démontrant ainsi de manière directe la quantification du champ électromagnétique,[28][29] de sorte que la prédiction d'Einstein est considérée comme prouvée.
Prix Nobel en lien avec la notion de photon
Le lecteur intéressé par l'histoire des idées est invité à se reporter aux textes des conférences Nobel, vivants témoignages de la science en mouvement (voir également la dualité onde-corpuscule dans les archives Nobel).
Prix Nobel attribués en lien avec la notion de photon :
- 1918 : Max Planck "in recognition of the services he rendered to the advancement of Physics by his discovery of energy quanta"
- 1921 : Albert Einstein "for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect"
- 1923 : Robert A. Millikan "for his work on the elementary charge of electricity and on the photoelectric effect"
- 1927 : Arthur H. Compton "for his discovery of the effect named after him" (partagé avec Charles Thomson Rees Wilson)
- 1965 : Sin-Itiro Tomonaga, Julian Schwinger et Richard P. Feynman "for their fundamental work in quantum electrodynamics, with deep-ploughing consequences for the physics of elementary particles"
- 2005 : Roy J. Glauber "for his contribution to the quantum theory of optical coherence" (partagé avec John L. Hall et Theodor W. Hänsch)
Propriétés physiques
Le photon est sans masse, n'a pas de charge électrique[30] et ne se désintègre pas de façon spontanée dans le vide. Un photon a deux états de polarisation possibles et est décrit par trois paramètres continus: les composantes de son vecteur d'onde, qui déterminent sa longueur d'onde λ et sa direction de propagation. Les photons sont émis à partir de plusieurs processus, par exemple lorsqu’une charge est accélérée, quand un atome ou un noyau saute d’un niveau d'énergie élevé à un niveau plus faible, ou quand une particule et son antiparticule s'annihilent. Des photons sont absorbés par le processus inverse, par exemple dans la production d’une particule et de son antiparticule ou dans les transitions atomique et nucléaire vers des niveaux d’énergie élevés.
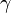
) entre un positron et un électron.Comme le photon est sans masse, il se déplace dans le vide à la vitesse c (la vitesse de la lumière dans le vide) et son énergie E et la quantité de mouvement p sont reliées par E = c•p. En comparaison, l’équation correspondante pour des particules de masse invariable m serait 
, comme démontré en relativité restreinte.
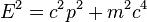
L’énergie et la quantité de mouvement dépendent seulement de sa fréquence ν, ou de façon équivalente, sa longueur d’onde λ :
Et conséquemment la quantité de mouvement est
où 
( constante de Dirac ou constante de Planck réduite); 
est le vecteur d’onde (avec le nombre d’onde 
comme amplitude) et 
est sa fréquence angulaire. Noter que pointe dans la direction de propagation du photon. Le photon est aussi caractérisé par son spin qui est indépendant de sa fréquence. L'amplitude du spin est 
et la composante mesurée dans la direction de propagation, son hélicité, doit être 
. Les deux hélicités possibles correspondent aux deux états possibles de polarisation circulaire du photon (horaire et anti-horraire).
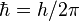
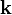
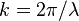
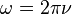
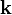
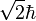
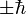
Pour illustrer l’importance de ces formules, l’annihilation d’une particule et de son antiparticule doit avoir pour résultat la création d’au moins deux photons pour les raisons suivantes. Dans le référentiel du centre de masse, les particules entrant en collision n'ont pas de quantité de mouvement, alors qu’un seul photon a toujours une certaine quantité de mouvement. La loi de conservation de la quantité de mouvement nécessite donc qu’au moins deux photons soient créés, avec une quantité de mouvement nette nul. L’énergie des deux photons peut être déterminée en respectant les lois de conservation. Le processus inverse, la création de paires, est le mécanisme dominant par lequel des photons de haute énergie (comme les rayons gamma) perdent leur énergie en passant à travers la matière.
Les formules classiques de l’énergie et de la quantité de mouvement des radiations électromagnétiques peuvent être ré-exprimés en terme d’évènements reliés aux photons. Par exemple, la pression des radiations électromagnétiques sur un objet provient du transfert de quantité de mouvement des photons par unité de temps et de surface de cet objet.
Modèles
Bille de lumière
La première image que l'on a du photon est la " bille de lumière ", la lumière serait composée de grains qui voyageraient à 299 792 458 m/s (Vitesse de la lumière).
Dans ce modèle, un flux d'énergie lumineuse donné est décomposé en billes dont l'énergie dépend de la longueur d'onde λ et vaut h.c/λ. Ainsi, pour une lumière monochromatique (c'est-à-dire dont le spectre se résume à une seule longueur d'onde), le flux d'énergie est composé en beaucoup de " petites " billes si la longueur d'onde est grande (du côté du rouge), ou de peu de " grosses " billes si la longueur d'onde est petite (du côté du bleu) — les qualificatifs " petit " et " gros " ne sont pas relatifs à la taille des billes, mais à la quantité d'énergie qu'elles comportent.
Si la lumière est composée de plusieurs longueurs d'onde, alors le flux d'énergie se compose de billes de " grosseurs " diverses.
Cette vision, simpliste selon les normes actuelles, ne permet pas d'expliquer correctement toutes les propriétés de la lumière.
Paquet d'onde
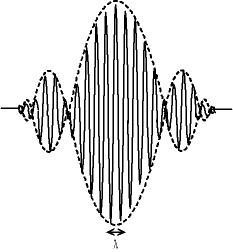
On peut représenter au premier abord les photons par des paquets d'onde : l'onde électromagnétique n'est pas une sinusoïde d'extension infinie, il y a une enveloppe d'amplitude importante encadrée par d'autres enveloppes nettement moins significative.
Ce modèle est insuffisant. En effet, dans une telle configuration, le photon devrait s'élargir au fur et à mesure de sa progression (on parle de l'" étalement du paquet d'onde "), l'énergie devrait être de moins en moins concentrée. Or, on constate que même après un trajet interstellaire de plusieurs milliers d'années-lumière, les propriétés des photons sont exactement les mêmes.
Dualité onde-corpuscule
Le photon est un concept pour expliquer les interactions entre les rayonnements électromagnétiques et la matière. Comme pour les autres particules élémentaires, il a une dualité onde-particule. On ne peut parler de photon en tant que particule qu'au moment de l'interaction. En dehors de toute interaction, on ne sait pas — et on ne peut pas savoir — quelle " forme " a ce rayonnement. On peut imaginer que le photon serait une concentration qui ne se formerait qu'au moment de l'interaction, puis s'étalerait, et se reformerait au moment d'une autre interaction. On ne peut donc pas parler de " localisation " ni de " trajectoire " du photon.
On peut en fait voir le photon comme une particule quantique, c'est-à-dire un objet mathématique défini par sa fonction d'onde qui donne la probabilité de présence. Attention à ne pas confondre cette fonction et l'onde électromagnétique classique.
Ainsi, l'onde électromagnétique, c'est-à-dire la valeur du champ électrique et du champ magnétique en fonction de l'endroit et du moment (
et 
), a donc deux significations :
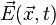
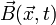
- macroscopique : lorsque le flux d'énergie est suffisamment important, ce sont les champs électrique et magnétique mesurés par un appareil macroscopique (par exemple antenne réceptrice, un électroscope ou une sonde de Hall) ;
- microscopique : elle représente la probabilité de présence des photons, c'est-à-dire la probabilité qu'en un endroit donné il y ait une interaction quantifiée (c'est-à-dire d'une énergie hν déterminée).
Propriétés générales
De la lumière monochromatique de fréquence ν est constituée de photons d'énergie E :
et de quantité de mouvement (ou impulsion) p :
h étant la constante de Planck (h = 6,626.10 − 34), c la vitesse de la lumière dans le vide (c = 3.108) et λ la longueur d'onde tel que 
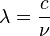
Il faut lever ici un paradoxe apparent : si le photon est monochromatique (une seule longueur d'onde λ), cela devrait être une sinusoïde infinie ; on ne peut obtenir un paquet d'onde que si l'on a un spectre d'une certaine largeur (par exemple de type gaussien). En fait, comme tout phénomène quantique, il y a une incertitude sur l'impulsion p (donc une certaine largeur de spectre) et sur la position x. Le photon ne représente donc qu'une seule longueur d'onde (celle du maximum du spectre, la sinusoïde inscrite dans l'enveloppe), mais est en fait décomposable en une superposition de sinusoïdes de longueurs d'onde voisines (via une transformée de Fourier).
Le photon respecte le principe d'incertitude d'Heisenberg : si l'on connaît avec précision sa position (c'est-à-dire que le paquet d'onde est étroit, δx est faible), alors l'incertitude sur sa quantité de mouvement p, qui se traduit par une dispersion de longueur d'onde δλ, est importante, car dépendant de 1/δx.
On peut relier ceci avec l'étalement du paquet d'onde : au moment de l'interaction, le photon est bien localisé (δx petit) donc la dispersion de la quantité de mouvement est grande (δλ grand). L'instant d'après, la dispersion de quantité de mouvement fait que le photon est moins bien localisé, il s'étale (δx est plus grand) ; sa " forme " s'étant " rapprochée " de la sinusoïde idéale, son spectre s'est rétrécit (δλ est plus petit). On peut voir grossièrement δx comme le " diamètre " du photon.
Lorsqu'ils se déplacent dans la matière, les photons se déplacent plus lentement que dans le vide, la vitesse étant déterminée par la valeur de l'indice de réfraction de ce milieu, qui lui-même dépend de la fréquence ou la longueur d'onde de cette lumière.
Selon les connaissances du XXIe siècle, les photons sont des particules élémentaires d'énergie bien déterminée et de masse au repos nulle. Selon la théorie de la relativité générale, les photons, malgré leur masse au repos nulle, sont soumis à la gravitation puisqu'ils possèdent une énergie non nulle (équivalence masse énergie). Ceci a pu être confirmé par des observations, les plus spectaculaires étant les lentilles ou mirages gravitationnels. Notamment, à l'occasion d'une éclipse solaire, on a pu constater que l'image des étoiles se déplaçait lorsque le Soleil passait à proximité de cette image ; ceci s'explique par le fait que la trajectoire des photons est modifiée par la proximité du Soleil. Cette observation, faite en 1919, est une des première confirmations expérimentales de la théorie de la relativité générale.
Notes et références
- ↑ a b c d Einstein, A (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt (trans. A Heuristic Model of the Creation and Transformation of Light)". Annalen der Physik 17: 132–148. (de). An English translation is available from Wikisource.
- ↑ a b Einstein, A (1909). "Über die Entwicklung unserer Anschauungen über das Wesen und die Konstitution der Strahlung (trans. The Development of Our Views on the Composition and Essence of Radiation)". Physikalische Zeitschrift 10: 817–825. (de). An English translation is available from Wikisource.
- ↑ Einstein, A (1916a). "Strahlungs-emission und -absorption nach der Quantentheorie". Verhandlungen der Deutschen Physikalischen Gesellschaft 18: 318. (de)
- ↑ a b Einstein, A (1916b). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Geselschaft zu Zürich 16: 47. Also Physikalische Zeitschrift, 18, 121–128 (1917). (de)
- ↑ La matière quant à elle est constituée de fermions, comme, entre autres, les quarks dont sont faits les noyaux atomiques, et les électrons qui leur sont liés.
- ↑ pour autant, il y a plus d'atomes dans l'eau qui coule d'un robinet pendant 1 seconde que de photons perçus par la rétine au cours de la même durée lors d'un clair de Lune
- ↑ Lewis, GN (1926). "The conservation of photons". Nature 118: 874–875.
- ↑ Villard, P (1900). "Sur la réflexion et la réfraction des rayons cathodiques et des rayons déviables du radium". Comptes Rendus 130: 1010–1012.
- ↑ Villard, P (1900). "Sur le rayonnement du radium". Comptes Rendus 130: 1178–1179. (fr)
- ↑ Rutherford, E; Andrade ENC (1914). "The Wavelength of the Soft Gamma Rays from Radium B". Philosophical Magazine 27: 854–868.
- ↑ René Descartes, Discours de la méthode, 1637
- ↑ Robert Hooke, Micrographia: or some physiological descriptions of minute bodies made by magnifying glasses with observations and inquiries thereupon..., 1665
- ↑ Christian Huygens, Traité de la lumiere, 1678
- ↑ Isaac Newton, Opticks, Dover Publications, 1730, Book II, Part III, Propositions XII–XX; Queries 25–29 p.
- ↑ Jed Z. Buchwald, The Rise of the Wave Theory of Light: Optical Theory and Experiment in the Early Nineteenth Century, University of Chicago Press, 1989
- ↑ Maxwell, JC (1865). "A Dynamical Theory of the Electromagnetic Field". Philosophical Transactions of the Royal Society of London 155: 459–512. Cet article suit une présentation par Maxwell à la Royal Society le 8 décembre 1864.
- ↑ Hertz, H (1888). "Über Strahlen elektrischer Kraft". Sitzungsberichte der Preussischen Akademie der Wissenschaften (Berlin) 1888: 1297–1307. (de)
- ↑ Wilhelm Wien Nobel Lecture. du 11 décembre 1911.
- ↑ Planck, M (1901). "Über das Gesetz der Energieverteilung im Normalspectrum". Annalen der Physik 4: 553–563. (de)
- ↑ Max Planck's Nobel Lecture. du 2 juin 1920.
- ↑ a b Robert A. Millikan's Nobel Lecture. du 23 mai 1924.
- ↑ Compton, A (1923). "A Quantum Theory of the Scattering of X-rays by Light Elements". Physical Review 21: 483–502.
- ↑ Zeilinger, Anton (2000). "The quantum centennial". Nature 408: 639–641.
- ↑ a b Mandel, L. (2000). "The case for and against semiclassical radiation theory". Progress in optics XIII: 27–68.
- ↑ Bohr, N; Kramers HA and Slater JC (1924). "The Quantum Theory of Radiation". Philosophical Magazine 47: 785–802. Également dans Zeitschrift für Physik, 24, 69 (1924).
- ↑ A Pais, Subtle is the Lord: The Science and the Life of Albert Einstein, Oxford University Press, 1982
- ↑ Ces expériences produisent des corrélations qui ne peuvent être expliquées par une théorie classique de la lumière, puisqu'elles résultent du processus quantique de la mesure. En 1974, Clauser a montré une violation d'une inégalité de Cauchy-Schwarz classique (Phys. Rev. D 9:853). En 1977, Kimble et ses collaborateurs ont démontré un effet de dégroupement de photons à l'aide d'un interféromètre Hanbury Brown et Twiss, alors qu'une approche classique montrerait un groupement des photons (Phys. Rev. Lett. 39:691). Cette approche a également été suivie par Grangier et ses collaborateurs en 1986 (Europhys. Lett. 1:501). Voir également la discussion et les simplifications faites par Thorn et al., Am. J. Phys. 72:1210 (2004).
- ↑ Brune, M; Schmidt-Kaler F, Maali A, Dreyer J, Hagley E, Raimond JM, and Haroche S (1996). "Quantum Rabi Oscillation: A Direct Test of Field Quantization in a Cavity". Phys. Rev. Lett. 76: 1800–1803.
- ↑ Gleyzes, S; Kuhr S, Guerlin C, Bernu J, Deléglise S, Busk Hoff U, Brune M, Raimond JM, and Haroche S (2007). "Quantum jumps of light recording the birth and death of a photon in a cavity". Nature 446: 297–300.
- ↑ Kobychev, V V; Popov, S B (2005). "Constraints on the photon charge from observations of extragalactic sources". Astronomy Letters 31: 147–151. DOI:10.1134/1.1883345.