Quadrivecteur - Définition

La théorie de la relativité (restreinte, puis générale) postulée par Einstein amène à considérer les trois coordonnées d'espace (par exemple hauteur, largeur, profondeur) et le temps comme formant un tout indissociable.

La description et les calculs sur cet ensemble (baptisé depuis espace-temps) ont amené Einstein à prolonger la notion de vecteur newtonien classique (formé de trois coordonnées d'espace, tel le vecteur vitesse d'un point matériel) pour créer un nouvel objet mathématique, le quadrivecteur.

Un quadrivecteur correspond donc à l'ensemble de non pas trois mais quatre composante, la composante supplémentaire étant associée à la coordonnée de temps t. Pour des raisons dimensionnelles, on utilise parfois à sa place la coordonnée, éeventuellement notée x⁰ égale au produit de la coordonnée de temps par la vitesse de la lumière, c t. Selon les cas, le temps apparaît soit en premier (comme le suggère la notation x⁰), soit en dernier. La raison d'être des quadrivecteur est tout d'abord de décrire comment se transforme l'ensemble des coordonnées x, y, z et t (ou c t) lors d'un changement de référentiel. Ces changements sont appelés transformation de Lorentz en relativité restreinte.

Par extension, il apparaît qu'un grand nombre de quantités peuvent être vues comme se transformant comme les quatre coordonnées d'espace-temps. De tels objets sont également des quadrivecteurs. Les composantes spatiales des quadrivecteurs correspondent toujours à un vecteur tridimensionnel en mécanique classique. La signification physique de la quatrième composante des quadrivecteurs est par contre moins immédiate, quoique toujours en rapport avec l'objet considéré.

Quadrivecteurs covariants et contravariants

Un quadrivecteur peut exister sous deux formes, dites covariante et contravariante. La distinction entre ces deux formes se fait à l'aide de la position des indices des composantes de quadrivecteurs.

Quand les indices sont notés en exposant, on parle d'indices covariants. Quand il sont notés en bas, on parle d'indices contravariants. Par exemple, pour un vecteur V :

• Les V^a sont les composantes covariantes du vecteur,
• Les V_a sont les composantes contravariantes du vecteur.

Les coordonnées x, y, z et t sont des quantités covariantes. On les note ainsi sous la forme

(t,x,y,z) = x^a.

Il est possible de passer de la forme covariante à la forme contravariante des composantes d'un vecteur à l'aide d'une opération qui peut formellement s'assimiler à une multiplication matricielle, à l'aide d'une matrice symétrique en général notée η_ab. On a ainsi, pour tout vecteur

. Dans ce genre de sommation, il est de coutume d'omettre le signe somme, celle-ci étant implicite chaque fois qu'un inidie apparaît simultanément en haut et en bas dans une formule. L'équation précédente se note ainsi

V_a = η_abV^b.

La transformation inverse se fait à l'aide de la matrice inverse, notée avec des indices en haut,

.

On a ainsi

V^a = η^abV_b.

La matrice η est appelée métrique de Minkowski. Sa forme matricielle est

.

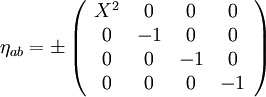
La quantité X vaut c (la vitesse de la lumière) ou 1 selon que la coordonnée temporelle a été prise égale à t ou c t. Le signe de η est indéterminé, et dépend d'une convention arbitraire, appelée convention de signe de la métrique.

En règle générale, un quadrivecteur est défini de façon non ambiguë par sa forme covariante ou contravariante, l'autre forme étant déduite par l'action de la matrice η.

La matrice η permet de calculer la norme d'un quadrivecteur, ou plus généralement le produit scalaire entre deux vecteur. On a ainsi

.

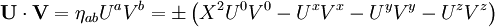
Quelques exemples de quadrivecteurs

• Quadrivecteur position-temps:

,

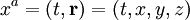
ou

.

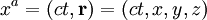
• Quadrivecteur vitesse (quadrivitesse) :

,

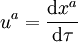
ou

,

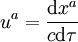
où τ est le temps propre, c'est-à-dire le temps qui serait indiqué par une horloque qui serait attaché à l'objet dont la trajectoire aurait le vecteur vitesse correspondant. Le quadrivecteur vitesse est par définition de norme fixée (par norme on entend la quantité η_abu^au^b, voir paragraphe ci-dessus), égale, selon la convention de coordonnée et de signe choisie à c², -c², 1, ou -1. La composante temporelle du quadrivecteur vitesse est déterminée par la condition que la norme soit égale à la valeur imposée.

• Quadrivecteur impulsion (quadriimpulsion). Pour une particule de masse non nulle :

,

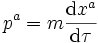
ou

,

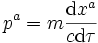
où τ est le temps propre. Le quadrivecteur impulsion possède une norme fixée, égale, selon la convention de coordonnée et de signe choisie à m²c², -m²c², m², ou -m². La composante temporelle du quadrivecteur vitesse est déterminée par la condition que la norme soit égale à la valeur imposée. On peut montrer qu'elle s'idenfie (à une constante près) à l'énergie de l'objet telle qu'elle serait mesurée par un observateur immobile par rapport aux coordonnées x, y, z.

• Potentiel vecteur A_a. Ce quadrivecteur est défini avec des composantes contravariantes. Ses composantes spatiales s'identifient (au signe près) au potentiel vecteur de l'électromagnétisme, dont le rotationnel donne le champ magnétique. Sa composante temporelle donne, à un facteur multiplicatif près, le potentiel électrique.